Transforme para o sistema de coordenadas polares a integral
Em seguida, calcule o seu valor.
Passo 1
Vamos lembrar como convertemos as coordenadas cartesianas para polares:
Então vamos reescrever a função que estamos integrando:
Lembrando que , ficamos com:
Beleza, convertemos a função.
Passo 2
O segundo passo é achar os novos limites de integração para e para . Para isso, é uma boa esboçar a região de integração original.
Pela integral do enunciado, vemos que varia no intervalo:
E para cada um desses valores de , o varia no seguinte intervalo:
Vamos desenhar isso no plano (é uma boa ideia lembrar que é a metade superior de um círculo, assim como é a metade inferior, porque essa função aparece com muita frequência nessa matéria):
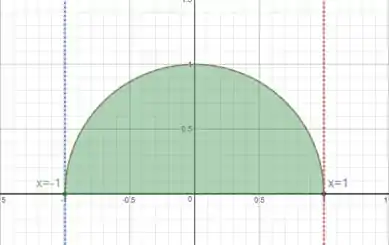
Olhando para essa imagem, fica muito mais fácil entender como o e o variam!
Como temos um círculo de raio :
E como estamos percorrendo toda a metade superior do círculo:
Passo 3
O terceiro passo é “converter” aqueles diferenciais para coordenadas polares. Para isso precisamos usar o famoso “jacobiano”.
No caso das coordenadas polares, sabemos que:
Agora já podemos substituir tudo na integral:
Passo 4
Ok, terminamos a conversão, agora precisamos calcular a nova integral.
Precisamos usar uma substituição simples:
E com essa troca, precisamos calcular os novos limites de integração:
Então:
Podemos cortar o e tirar a constante de dentro da integral:
Passo 5
Agora já podemos integrar em relação a , lembrando que:
Então:
Agora é só integrar em relação ao :
Pronto!
Resposta
Letra (a).