- Inverta a ordem de integração (Tipo I para tipo II) e calcule:
- Usando coordenadas polares calcule:
Passo 1
Temos aqui uma questão de integral dupla que nos pede para resolvê-la em duas etapas: primeiro, mudar o sistema de coordenadas para coordenadas polares, e segundo, resolver a integral propriamente dita.
Mudanças deste tipo ficam muito mais fáceis de serem realizadas se nós entendermos qual é a nossa região. Mudar a função de integração é fácil só fazer a seguinte mudança:
Agora, mudar os limites de integração já é outro problema. Sendo assim, nosso primeiro passo é entender qual é a região de integração que estamos trabalhando.
De cara já sabemos que a nossa integral está montada no formato do tipo 1 (basta verificar que integramos primeiro em e depois em , só ver a ordem ).
Desta forma, como temos uma integral do tipo I, sabemos que a nossa região está limitada acima pela curva e abaixo pela reta (limites de integração da integral mais interna).
Para fecharmos a nossa região, falta as suas laterais. Então, da integral mais externa, temos que ela é limitada a esquerda pela reta e limitada a direita pela reta .
Ao fazermos esboço dessa região, teremos:
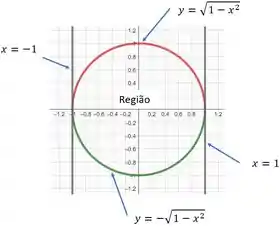
Passo 2
Agora que nós conseguimos visualizar a nossa região, fica muito mais fácil mudar a ordem de integração.
Como podemos ver, a região consiste em um círculo de raio e centrada na origem . Sendo assim, nossos limites devem englobar toda essa região do círculo.
Portanto, eles são: e .
Agora, se no lugar de e da nossa nós colocarmos a relação que escrevemos no Passo 1, e , vamos obter:
Portanto, a nossa integral será:
Tomem muito cuidado na hora de mudar os limites para não esquecerem de mudar os diferenciais por viu!!!
Passo 3
Por fim, só nos resta resolvermos a nossa integral. Começando a integração pela variável , temos:
OBS: não conseguiu resolver a integral em relação a ? Não se assuste! Uma substituição simples resolve o seu problema. Se fizermos , teremos . Quando , . Já quando , teremos . Portanto, teríamos a seguinte integral.
E agora fica mais fácil de resolver né? Podem checar que o resultado será o mesmo que obtivemos antes!
Mas, vamos continuar para finalizar a questão. A nossa última integral é:
E assim finalizamos a questão!