Calcular a área da região abaixo usando integral dupla
Passo 1
Bom, antes de tudo vamos fazer um esboço dessa região para entender melhor o que está acontecendo e depois partimos para integral.
Começando pela inequação:
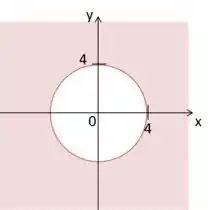
Essa é uma circunferência de raio centrada na origem e, como vemos pela inequação (o sinal ), a região que queremos está fora dela (indicado em vermelho no gráfico abaixo).
Passo 2
Temos também a seguinte inequação:
Que curva é essa? Se não fosse pelo termo , você pensaria direto em uma circunferência, não é? E realmente é um circunferência, esse termo apenas nos diz que ela não está centrada na origem.
Sempre que você vir uma equação desse tipo, com um termo quadrático e um simples da mesma variável (e ) é uma boa tentar juntar esses termos, completando o quadrado que eles formam. Como assim?
Queremos escrever o termo na forma , completando o que for necessário. Desenvolvendo esse quadrado, temos:
Se nós fizermos , temos:
Esses dois primeiros termos estão presentes na nossa inequação, o último não, mas beleza. Vamos substituir por , mas como sinifica adicionar um termo que não estava lá antes, vamos retirar esse termo, ok? Olha só:
Assim não alteramos a inequação, certo? Beleza, então temos:
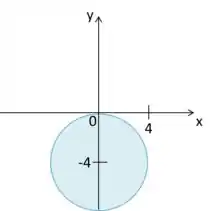
Isso é uma circunferência de raio , como previmos, não centrada na origem (ela está centrada em ). Como vemos pela inequação (o sinal ) a região que queremos está dentro dela.
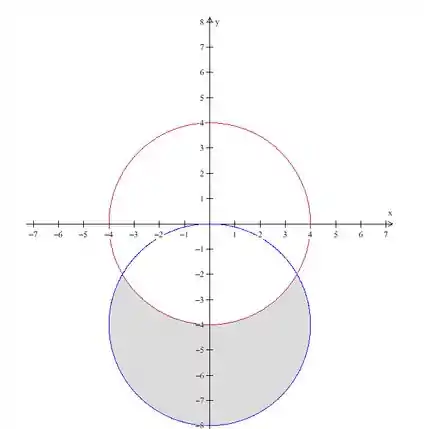
Portanto, juntando os dois gráficos temos isso aqui:
Passo 3
Como nós queremos a área da região, precisamos resolver a seguinte integral:
Onde é a região marcada em cinza na figura.
Como a região é limitada por círculos, vamos usar coordenadas polares aqui:
Sempre que mudamos de coordenadas nas integrais duplas, precisamos calcular o Jacobiano dessa transformação, neste caso temos
A equação da circunferência vermelha se transforma então em . Veja,
Agora vamos fazer essa substituição na outra circunferência :
Passo 4
Beleza, agora vamos olhar um pouco para a figura. Repare que, dentro da nossa região , temos o raio variando desde a circunferência vermelha até a azul, portanto:
Não está errado esse sinal não? Não, porque abaixo do eixo , tem valores negativos, portanto, é um número positivo.
Beleza, agora vamos analisar o intervalo de . Antes de sair chutando, dá uma olhada de novo a figura da nossa região . Lembra que é marcado em relação à parte positiva do eixo ? Queremos então esses ângulos aqui em amarelo:
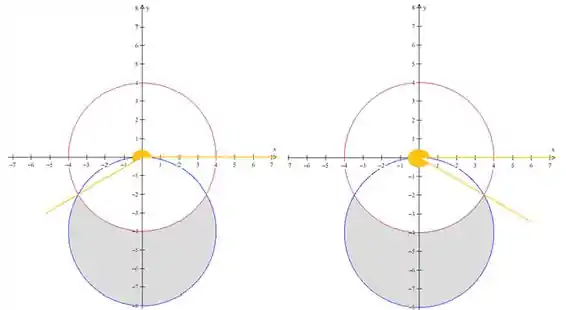
Mas como vamos descobrir esses ângulos? Bom, esses ângulos batem exatamente na interseção das duas curvas né? Então que tal acharmos essa interseção! Vamos começar substituindo logo e nas funções:
Substituindo na primeira equação:
E qual ângulo têm o seno igual a ? . Mas aqui estamos abaixo do eixo .
Então primeiro temos,
Mas também vamos ter,
Logo, chegamos à conclusão de que
Passo 5
Nós descobrimos então que, em coordenadas polares, podemos escrever essa região como:
Vamos então fazer finalmente essa substituição polar na integral (não se esqueça do Jacobiano):
Passo 6
Agora vamos integrar isso aí em relação a :
Passo 7
Agora integramos em relação a , mas antes disso, precisamos nos lembrar da seguinte relação:
Isso nos dá
Agora vamos lá:
Substituindo: