Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 271234567891011121314151617181920212223242526282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UnB, Sem Campus, Cálculo 2, P3 - 2008.2, Questão 1

Sejam a ,   b ∈ R . Transformar em coordenadas cartesianas e descrever a seguinte curva, dada em coordenadas polares por

r = f θ = a cos ⁡ θ + b sin ⁡ θ ,                         0 ≤ θ ≤ π .

Passo 1

Fala, galera! Vamos resolver essa questão!

O enunciado pediu pra gente transformar a equação que tá em coordenadas polares para coordenadas cartesianas. Pra isso, nós vamos usar as relações:

x = r cos ⁡ θ

y = r sin ⁡ θ

r 2 = x 2 + y 2

Assim, vamos isolar as variáveis que estão presentes na nossa equação na forma polar e vamos obter algo em função de x e y .

Vamos lá!

Passo 2

Vamos começar isolando o cosseno na equação x = r cos ⁡ θ :

cos ⁡ θ = x r

Fazendo a mesma coisa com o seno em y = r sin ⁡ θ , temos:

sin ⁡ θ = y r

Substituindo as duas relações em r = a cos ⁡ θ + b sin ⁡ θ , vamos obter:

r = a x r + b y r

r = a x + b y r

Isolando r , temos:

r 2 = a x + b y

Substituindo r 2 = x 2 + y 2 na equação, temos na forma cartesiana:

x 2 + y 2 = a x + b y

Essa equação descreve uma circunferência, como a gente pode verificar plotando o gráfico de r = a cos ⁡ θ + b sin ⁡ θ para 0 ≤ θ ≤ π :

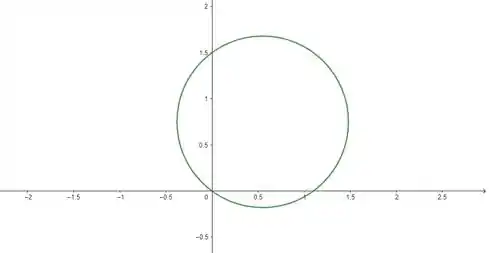
Como a e b são números reais, dependendo do valor que essas variáveis assumem nossa circunferência vai se deslocar horizontal ou verticalmente no gráfico, mas nunca deixa de ser uma circunferência.

Valeu, galera! Até a próxima! 😉

Resposta

x 2 + y 2 = a x + b y

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}