Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 191234567891011121314151617182021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFRJ. Cálculo 3. PF. 2022.1. Questão 1.

Calcule a integral

∫ ∫ D arctan ⁡ y x d A

onde a região D = x , y ∈ R 2 4 ≤ x 2 + y 2 ≤ 9 ,   0 ≤ y ≤ x .

Passo 1

Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Nessa questão temos uma integral da função arctan ⁡ y x dentro da região D , onde é limitada pelas circunferências x 2 + y 2 = 4 , x 2 + y 2 = 9 e as retas y = 0 e y = x .

Lembra que quando a região de integração tem uma circunferência certamente temos que usar coordenadas polares para resolver a integral? 😁

Como as circunferências em D estão centradas na origem, não precisamos transladar nossas coordenadas.

Convertendo nossas coordenadas para coordenadas polares, temos que fazer as seguintes mudanças

x = r c o s θ y = r s e n θ

Vamos começar nosso probleminha? 😉

Passo 2

Desenhando as curvas que limitam a região D , temos

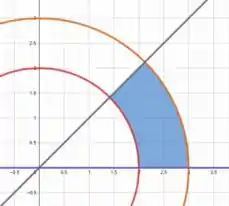
Assim podemos ver que a variação angular é de θ = 0 a θ = π / 4

Com isso, nossa função de integração será

arctan ⁡ r s e n θ r c o s θ → arctan ⁡ tan ⁡ θ

Como o a r c t a n é o inverso da t a n e estamos no primeiro quadrante, podemos escrever

arctan ⁡ tan ⁡ θ = θ

O ângulo entre as retas y = 0 e y = x é o ângulo que divide o primeiro quadrante em duas partes.

Já temos os limites de D para θ , 0 ≤ θ ≤ π / 4 .

Agora analisando as equações de circunferências

x 2 + y 2 = 4 x 2 + y 2 = 9  

Sabemos que a equação de uma circunferência é x 2 + y 2 = r 2 , então podemos observar que a variação de r é 2 ≤ r ≤ 3 .

Com essas informações podemos escrever nossa integral como (lembrando que nosso jacobiano é r )

∫ 0 π 4 ∫ 2 3 θ r d r d θ

Tranquilo até aqui? 😎

Passo 3

Primeiro integrando com relação a r pelo método de integração polinomial

∫ θ r d r = θ r 1 + 1 1 + 1 = θ r 2 2

Aplicando os limites de integração

∫ 2 3 θ r d r = θ 3 2 2 - θ 2 2 2 = 5 θ 2

Com base nesse resultado integramos com relação a θ pelo mesmo método anterior

∫ 5 θ 2 d θ = 5 θ 1 + 1 1 + 1 = 5 θ 2 2

Aplicando os limites de integração, temos

∫ 0 π 4 5 θ 2 d θ = 5 π 4 2 2 - 5 0 2 2

Fazendo a divisão das frações:

5 2 π 2 16 2 = 5 2 π 2 16 ∙ 1 2 = 5 π 2 64

Ou seja, a integral de arctan ⁡ y x dentro da região D é 5 π 2 64 !

É isso! Essa resolução te ajudou? Responde Aí! ✌

Resposta

∫ ∫ D arctan ⁡ y x d A = 5 π 2 64

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}