UFSCAR. Cálculo 3. Lista de Estudos – Integrais Duplas. Questão 5.
5 – Calcular:
Em que é a região do primeiro quadrante delimitada por , , e .
Passo 1
Falaaaaaa aí. Tudo certinho com você? Vem comigo resolver mais uma questão e garantir aquela aprovação de milhões.
E a primeira coisa que fazermos é entender direitinho esse enunciado aí.
Veja bem, essa questão pede pra gente calcular o valor dessa integral aqui:
Que parece até bonitinha, né. Mas ele fala pra gente calcular essa integral em uma região específica, e dá pra gente as relações que limitam essa região que ele chamou de região .
Em que é a região do primeiro quadrante delimitada por , , e .
Então, nós primeiro precisamos saber que região é essa, pra depois calcularmos de fato a integral, ok.
Vem comigo que eu te ajudo com isso
😉👍
Passo 2
Para resolver essa integral dupla, nós precisamos encontrar os limites de integração. Repara que o enunciado disse a região que estamos integrando está delimitada no primeiro quadrante por duas circunferências: a e a e por duas retas, a e a .
Como envolvem circunferências, uma boa ideia é usar coordenadas polares para definirmos esses limites. Isso vai ajudar bastante a facilitar os cálculos.
Então precisaremos fazer as seguintes mudanças para coordenadas polares:
Lembrando, que qualquer mudança de variável, implica em multiplicar a função da integral pelo Jacobiano. Nas coordenadas polares, o Jacobiano dessa transformação sempre será
Passo 3
Agora vamos analisar os intervalos de integração! O enunciado forneceu duas equações de circunferência:
A primeira corresponde a uma circunferência de raio igual a . Já a segunda, é uma circunferência de raio igual a .
O problema também diz que a região está limitada no primeira quadrante e pelas retas e .
Então a região que estamos estudando será essa abaixo:
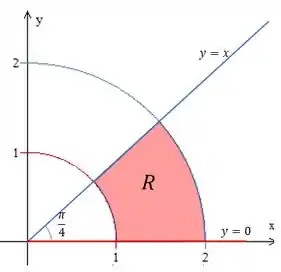
Repara que o raio varia entre e e o ângulo entre e .
Passo 4
Agora que encontramos os limites de integração, vamos substituir na integral. Lembrando que a integral que estamos resolvendo tem essa cara:
E que
Vamos, então, montar a integral, substituindo os valores que atribuímos a e :
Passo 5
Agora partiu resolver a integral!
Vamos começar usando o teorema de Fubini que diz que devemos integrar de dentro para fora, por isso vamos integrar primeiro em relação a . Então, podemos colocar o do lado de fora da integral e teremos:
E a integral do cosseno é o seno. Assim:
Sendo e . E nossa integral se torna:
Podemos colocar , já que é uma constante
E agora nos resta resolver essa última integral e correr para o abraço.
Que nos dá:
E prontinho, chegamos ao fim de mais uma questão. 😊