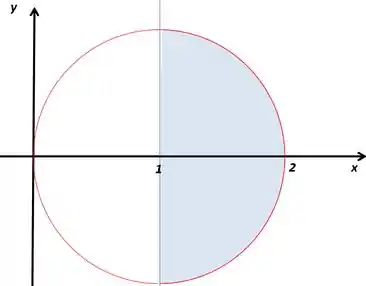
Considere a região plana dada por:
E a integral dupla
- Esboce a região
- Expresse a integral como uma integral iterada nas variáveis cartesianas e y, integrando primeiro com respeito a e em seguida com respeito a (Obs.: Neste item não é pedido o cálculo da integral).
- Expresse a integral como uma integral iterada nas variáveis polares e . (Obs.: Neste item não é pedido o cálculo da integral)
- Calcule (usando o método que preferir)
Passo 1
Antes de esboçarmos a região vamos entender o que ela é. Uma delas é a parte de dentro de uma circunferência
Completando quadrados
Isso é uma circunferência de raio e centro em , como ele quer a parte da direita da circunferência, porque passa no centro dela.
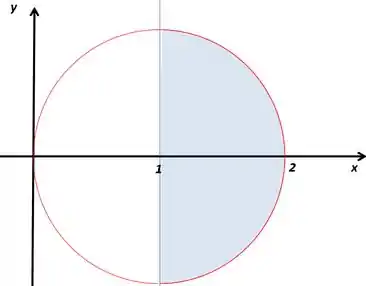
Passo 2
Para escrever a integral como ele quer precisamos ver qual intervalo de ele varia, e entre que funções de ele varia. Podemos ver que em , ele vai de à .
Em ele vai da parte de baixo da circunferência até a parte de cima dela. Vamos escrever isso
Podemos escrever assim
A integral fica
Passo 3
Vamos fazer por coordenadas polares agora, para isso faremos, então:
Passo 4
Vamos começar vendo como varia os ângulos, olha essa figura aqui embaixo
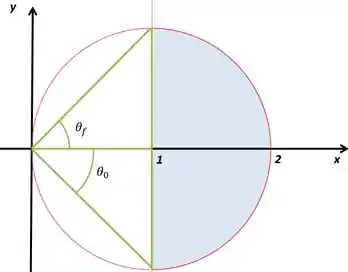
Repara que são dois triângulos iguais, os dois isósceles, então os ângulos vão ser
Lembra só do sinal hein, o inicial é negativo porque começamos a contagem então
Vamos ver agora o valor de . Repara que começa em , em coordenadas polares isso quer dizer
Ele termina na circunferência
Então vamos ter o sendo
A integral vai ficar
Passo 5
Dentre as duas integrais a das coordenadas polares é bem mais fácil, vamos resolve-la
Lembrando que