UFSCAR. Cálculo 3. Lista de Estudos – Integrais Duplas. Questão 6.
6 – Calcular:
Em que é a região delimitada por .
Passo 1
Fala aí! Tudo belezinha por aí? Vamos resolver mais essa questão juntos? Vem comigo!
Bem, o problema pediu pra gente calcular essa integral, que é uma integral dupla
E disse que é pra gente fazer isso em , que é a região delimitada por .
Bom, o primeiro passo será entender que região é essa, e para isso nós teremos que desenhá-la. Então bora fazer isso.
Passo 2
Vamos começar desenhando
Perceba que essa é a equação de uma elipse, e pra fazer as informações importantes aparecerem, temos que dar uma mexida nela. Vamos dividir tudo por , ficando com:
Simplificando, teremos:
Que pode ser escrita como:
Que é uma elipse centrada em e semieixos e
Desenhando, teremos:
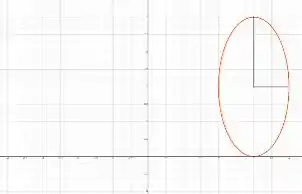
Xiii, temos um problema. Como podemos definir os limites de integração nessa região???
Bom, pra fazer isso nós vamos pensar o seguinte: do jeito que a elipse está, a gente não consegue integrar, então vamos fazer uma mudança de variáveis para transformar essa região em uma outra circunferência centrada na origem. Isso vai ajudar bastante a gente.
Bora fazer isso no próximo passo.
Passo 3
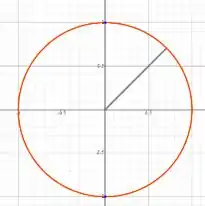
Vamos fazer uma mudança de variável usando nossa equação da circunferência
Que pode ser visto como:
Então chamaremos
E
Assim ficamos com:
Que é uma circunferência centrada na origem
Ahhhh, tem um detalhe bem importante aqui: como estamos fazendo uma mudança de variável, precisamos calcular o Jacobiano dessa transformação. Então precisamos fazer.
Assim,
E
Assim,
E o Jacobiano é dado por:
Com isso, nossa integral que era
Se transforma em
Agora vamos nos concentrar em resolver essa integral.
Passo 4
Podemos passar a integral para coordenadas polares, onde
E as variações de e podem ser vistas no gráfico como:
Transformando a integral em:
Caramba!!! Viu como todas essas manobras ajudaram a melhorar bastante a nossa integral?
Bora resolver, então.
Passo 5
Usando o Teorema de Fubini, vamos integral de dentro pra fora.
E prontinho. Integral resolvida.