Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 361234567891011121314151617181920212223242526272829303132333435373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFMG, Sem Campus, Cálculo 3, P1 - 2022.1, Questão 3.

Calcule ∭ E z x 2 + y 2 d V onde E é a região de R 3 interna ao cilindro x 2 + y 2 = 4 , externa ao cilindro x 2 + y 2 = 1 , limitada acima pelo semicone z = 3 x 2 + y 2 e abaixo pelo paraboloide z = x 2 + y 2 .

a) 27 π 4

b) 39 π 4

c) 10 π

d) 31 π 4

e) 81 π 4

Passo 1

Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍

Nesse problema queremos calcular a integral ∭ E z x 2 + y 2 d V limitada pelos cilindros x 2 + y 2 = 4 e x 2 + y 2 = 1 e pelos paraboloides z = 3 x 2 + y 2 e z = x 2 + y 2 .

Como fazemos isso? 👀

Pelo que vemos no problema, vamos precisar converter as coordenadas cartesianas para coordenadas cilindricas.

Pra isso, temos que fazer

x = r cos ⁡ θ y = r sen ⁡ θ z = z x 2 + y 2 = r 2 J = r

Bora começar! 😉

Passo 2

Se esboçássemos os gráficos das regiões que limitam nossa região, teríamos

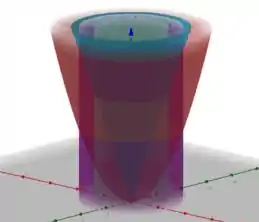
Nas figuras acima vemos a região e um corte da região em um plano x = 0 .

Primeiro vamos obter os limites de integração.

Estamos variando a altura da nossa integral em z entre 3 x 2 + y 2 e x 2 + y 2 .

Já o raio vemos que varia de 1 a 2 e o ângulo θ entre 0 e 2 π . Ou seja

∫ 0 2 π ∫ 1 2 ∫ x 2 + y 2 3 x 2 + y 2 z x 2 + y 2 d z r d r d θ

Calculando a primeira integral com relação a z , temos

∫ x 2 + y 2 3 x 2 + y 2 z x 2 + y 2 d z = z 2 2 x 2 + y 2 x 2 + y 2 3 x 2 + y 2

∫ x 2 + y 2 3 x 2 + y 2 z x 2 + y 2 d z = 3 x 2 + y 2 2 2 x 2 + y 2 - x 2 + y 2 2 2 x 2 + y 2

∫ x 2 + y 2 3 x 2 + y 2 z x 2 + y 2 d z = 9 ( x 2 + y 2 ) 2 x 2 + y 2 - x 2 + y 2 2 = 9 2 - x 2 + y 2 2

Substituindo esse resultado na integral, temos

∫ 0 2 π ∫ 1 2 9 - x 2 + y 2 2 r d r d θ

Nesse momento, temos que converter nossas coordenadas para polares fazendo as substituições que vimos no passo 1...

∫ 0 2 π ∫ 1 2 9 - r 2 2 r d r d θ

∫ 0 2 π ∫ 1 2 9 r - r 3 2 d r d θ

Tranquilo até aqui? 👀

Passo 3

Integrando com relação a r , temos

∫ 1 2 9 r - r 3 2 = 9 r 2 4 - r 4 8 1 2 = 9 2 2 4 - 2 4 8 - 9 1 2 4 - 1 4 8

∫ 1 2 9 r - r 3 2 = 39 8

E por fim, integrando o resultado em função de θ ...

∫ 0 2 π 39 8 d θ = 39 8 θ 0 2 π

∫ 0 2 π 39 8 d θ = 39 π 4

E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí

Resposta

b) 39 π 4

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}