UFCG – Cálculo 3 – Listas Moodle – 2022/1
6) Arraste e solte, nos campos correspondentes, o valor correto de cada elemento, conforme as opções disponíveis.
b) onde:
e ;
Passo 1
Falaaa... belezinha???
Repara que tem um e um , então nessa questão vamos fazer a mudança de variáveis para coordenadas polares.
Lembrando que, em coordenadas polares:
E temos também o jacobiano:
Passo 2
Vamos desenhar essa área de integração pra achar os limites de integração.
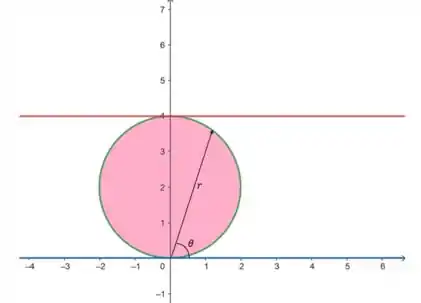
O varia de até .
Já o varia de até a equação do círculo, que é:
Em coordenadas esféricas:
Então o varia de até
Passo 3
Calculando o jacobiano:
Lembrando de trocar o que a gente ta integrando também:
Daí ficamos com a integral:
Resposta
Exercícios de Livros Relacionados
Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}