Provas antigas – Cálculo 2 – Unicamp – P2 6ª noite – questão 2
Calcule a integral
Passo 1
Faaaaaala, galera... Tranquileba?? Mogli na área 😊. Bora responder Aí essa questão?
O exercício nos pede para calcular uma integral que, eu, você ou alguém desatento poderíamos passar uma eternidade tentando resolver. Acontece que quando estamos fazendo integrais, especialmente as confusas, é bacana tentarmos olhar a integral por um outro ponto de vista, e isso é basicamente tentarmos visualizar a integral por outras coordenadas.
Mas antes, é bom termos uma noção das variáveis de integração. No nosso caso temos , mas é ou ? Nesse caso é , porque a o primeiro limite de integração depende de x.
Para isso, é interessante que façamos um esboço da região de integração, e temos algo nessa pegada:
Veja que temos uma região bidimensional e circular. Qual coordenada seria interessante aplicarmos?
As coordenadas polares, certo? Veja como elas são:
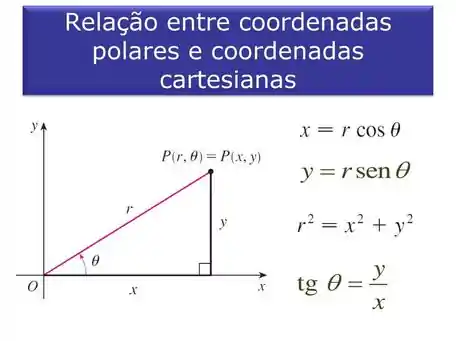
Onde agora as regiões de integração são e , então só temos que analisar a distância até a origem e em quais regiões o ângulo circula.
ATENTE-SE: quando fazemos uma troca de coordenadas, lembre-se que estamos olhando o problema por outra visão, então deve haver um aplicador que “ajeite” essa troca de coordenadas, ele é chamado de Jacobiano. É calculado, para o caso das coordenadas polares, dessa forma:
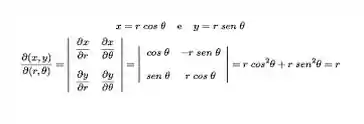
Então, vamos colocar um multiplicando dentro da integral.
“Então ok, sabemos que podemos olhar uma integral de diversas coordenadas. E uma vez achada a melhor coordenada, vamos aplicar e verificar os novos limites de integração para essa coordenadas, sem nos esquecermos do Jacobiano, certo, Mogli?” Isso mesmo, carinha.
Com a faca e o queijo em mãos, bora lá.
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Assim, veja pela imagem que:
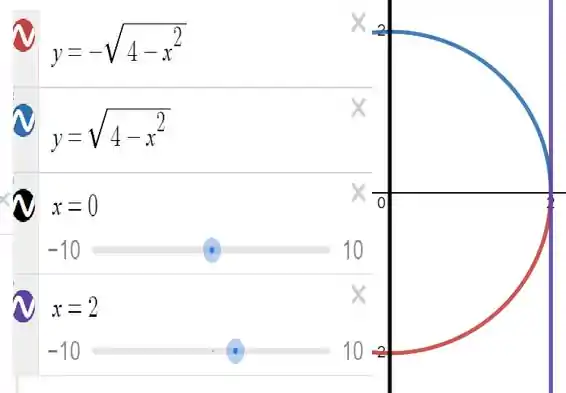
O raio vai de 0 até 2, e que o ângulo percorre de até . Assim, resumindo:
E analisando a função:
E sabendo que então:
Passo 3
De forma que a nossa integral fica:
O que multiplica é o Jacobiano.
Passo 4
Temos outro problema que é integral .
“Mas Mogli, é problema atrás de problema”. Sim, mas esse é fácil de resolver.
Como? Podemos usar uma substituição.
Façamos assim . E lembre-se, quando fazemos alguma substituição na integral, qualquer que seja, temos que verificar também como que ficam os novos limites de integração nessa substituição. Desse modo:
Assim a nossa integral fica:
E assim fica muito mais fácil. Integrando em u:
Veja que é constante para . Assim podemos tirá-lo da integração
Integrando em :
Assim, resumindo: