UTFPR, Cornélio Procópio, Cálculo 2, AVF - 2022.2, Questão 4
Calcule a integral, colocando-a em coordenada polar:
Onde é a região anular .
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu uma função, , e pediu pra gente calcular a integral dupla dela sobre a região , colocando em coordenada polar. Lembra das coordenadas polares? Ela tem essa cara:
E não podemos esquecer do Jacobiano da mudança, que é:
E olha que coisa linda, se a gente somar os quadrados dessas coordenadas polares, nós vamos ter:
Então nossa integral fica:
Já ficou mais bonitinho, né? Só falta a gente definir a região de integração, para escrever nossos limites e integrar.
Vamos lá!
Passo 2
O enunciado diz que nossa região é . Isso significa que ela é maior que a circunferência , de raio , e menor que a circunferência , de raio .
Então a gente tem isso aqui:
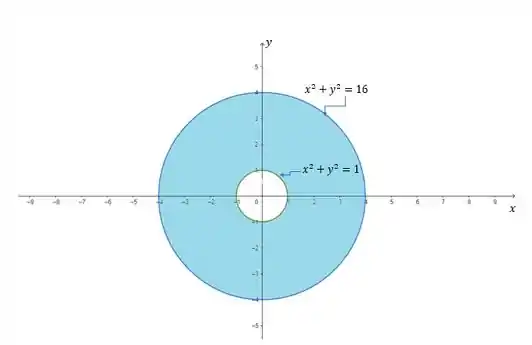
Beleza, então o nosso raio tá variando de a , enquanto nosso ângulo tá variando de a (uma volta completa na circunferência). Ou seja:
E aí nossa integral fica assim:
Passo 3
Vamos começar a calcular a integral em relação a fazendo uma mudança:
Não se esquecendo os limites:
Substituindo na integral, temos:
Colocando a constante do lado de fora da integral:
Integrando:
Aplicando os limites de integração:
Logo,
Integrando agora em relação a :
Aplicando os limites:
E encerramos o exercício. Valeu, galera! 😉