Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 411234567891011121314151617181920212223242526272829303132333435363738394042434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

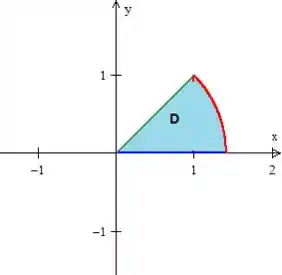
Questão 3:

Considere a região plana D = D 1 ∪ D 2 onde:

D 1 = x ,   y ∈ R 2 ,   0 ≤ x ≤ 1 ,   0 ≤ y ≤ x

e

D 2 = x ,   y ∈ R 2 ,   1 ≤ x ≤ 2 ,   0 ≤ y ≤ 2 - x 2

  1. Esboce D = D 1 ∪ D 2 e determine a fronteira de D através de igualdades e desigualdades.
  2. Calcule J = ��� D   ln ⁡ 1 + x 2 + y 2 d x d y

Passo 1

a )

Para esboçarmos a região pedida, vamos com calma! Sabemos que a região pedida D é a união de outras 2 , então vamos desenhar a primeira, D 1 ...

D 1 = x ,   y ∈ R 2 ,   0 ≤ x ≤ 1 ,   0 ≤ y ≤ x

Desenhar essa região aí, é primeiro desenhar as 4 curvas escondidas nessas desigualdades:

x = 0

x = 1

y = 0

y = x

Colocando essas 4 retas no plano, vamos obter...

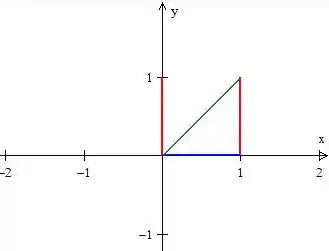
A região D 1 , é justamente a Região triangular no interior dessas 4 retas...

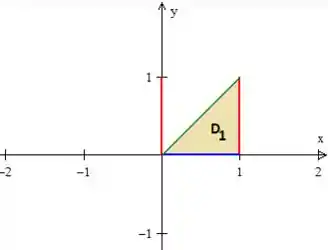
Passo 2

Vamos fazer a mesma coisa para a região D 2 ...

D 2 = x ,   y ∈ R 2 ,   1 ≤ x ≤ 2 ,   0 ≤ y ≤ 2 - x 2

Tirando as 4 curvas daí...

x = 1

x = 2

y = 0

y = 2 - x 2

As três de cima são retas. Inclusive, duas já estão desenhadas ( x = 1 e y = 0 ). Quanto a última curva...

y = 2 - x 2           →               y 2 = 2 - x 2         →

y 2 + x 2 = 2

Representa a parte de cima de uma circunferência de raio 2   (a parte de cima, pois a raiz está positiva):

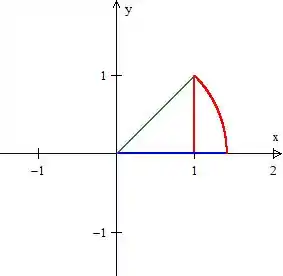
essas duas superfícies, D 1 e D 2 , juntas...

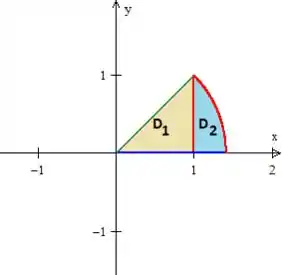
Chagamos na superfície D , que na verdade é um pedaço da circunferência de raio 2 ...

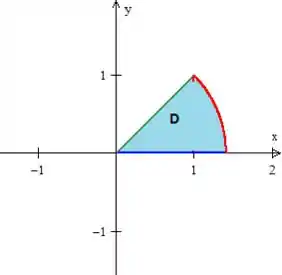
Pegou?

Passo 3

A outra parte do mesmo item pede para que indiquemos a fronteira da região D . Repare que a fronteira é dado por 3 curvas...

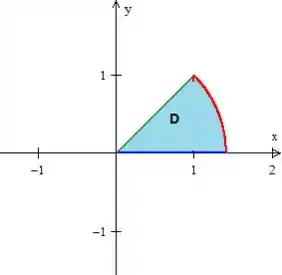
1º - Reta y = 0 , com o x variando de 0 até o raio máximo da circunferência...

0 ≤ x ≤ 2

2º - Reta y = x , com...

0 ≤ x ≤ 1

3º - Circunferência y = 2 - x 2 , com o x indo de 1 ≤ x ≤ 2 .

Passo 4

b )

O nosso intuito nesse item é calcular a integral dupla:

J = ∬ D   ln ⁡ 1 + x 2 + y 2 d x d y

Precisamos descrever a região D , o que não creio ser um grande problema, pois temos uma região que já sabemos ser circular... Ou seja, as coordenadas polares ajudam nesse item...

x = r cos ⁡ θ

y = r sin ⁡ θ

J = r

Uma equação que nos ajuda muito é a equação da circunferência...

x 2 + y 2 = r 2

Passo 5

Sim, não podemos sair de uma mudança sem dizer onde as coordenadas novas variam.

Repare que r , varia de 0 até o raio máximo da circunferência...

0 ≤ r ≤ 2

Já o ângulo θ , ângulo que sai do eixo x girando no sentido anti-horário positivo, sai da reta x = 0 e vai até a reta y = x ...

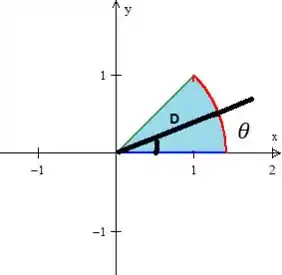
Na reta x = 0 , o ângulo é 0 , mas na reta y = x , pelas coordenadas polares...

y = x           →                 r sin ⁡ θ = r cos ⁡ θ         →

sin ⁡ θ cos ⁡ θ = 1           →             tan ⁡ θ = 1

Qual ângulo de 0 ° até 90 ° tem a tangente igual a 1 ?

θ = 45 ° = π 4

Então podemos afirmar que:

0 ≤ θ ≤ π 4

Passo 6

Pegando a integral...

J = ∬ D   ln ⁡ 1 + x 2 + y 2 d x d y

E substituindo as coordenadas polares não se esquecendo de multiplicar pelo Jacobiano...

J = ∫ 0 π 4 ∫ 0 2 ln ⁡ 1 + r 2 ⋅ J   d r d θ =

∫ 0 π 4 ∫ 0 2 ln ⁡ 1 + r 2 ⋅ r   d r d θ

Calculemos a integral de dentro...

∫ 0 π 4 ∫ 0 2 ln ⁡ 1 + r 2 ⋅ r   d r d θ

Podemos resolver essa integral fazendo uma substituição...

t = 1 + r 2           →                 d t = 2 r d r           →                     r d r = d t 2

Mudando também os limites de integração...

r = 0                 →                   t = 1 + 0 2 = 1

r = 2                 →                   t = 1 + 2 2 = 3

∫ 0 π 4 ∫ 0 2 ln ⁡ 1 + r 2 ⋅ r   d r d θ = 1 2 ∫ 0 π 4 ∫ 1 3 ln ⁡ t d t d θ

Vamos calcular essa integral separado, pois teremos que fazer por partes...

Passo 7

∫     ln ⁡ t d t

Tomando o ln ⁡   como a função para derivar e o d t para integrar...

u = ln ⁡ t

d v = d t

Calculando...

u = ln ⁡ t                 →                     d u = 1 t d t

d v = d t                       →                               v = t

Jogando na fórmula de integração por partes...

∫ u   d v = u v - ∫ v   d u

∫     ln ⁡ t d t = t ln ⁡ t - ∫ t ⋅ 1 t d t

Encontramos...

∫     ln ⁡ t d t = t ln ⁡ t - t

Passo 8

Substituindo esse resultado na integral iterada lá do passo 7 ...

1 2 ∫ 0 π 4 ∫ 1 3 ln ⁡ t d t d θ = 1 2 ∫ 0 π 4 t ln ⁡ t - t 1 3 d θ =

3 ln ⁡ 3 - 3 - 1 ln ⁡ 1 - 1 2 ∫ 0 π 4 d θ =

3 ln ⁡ 3 - 2 π 8

Resposta

a )

y = 0 ;         0 ≤ x ≤ 2 y = x ;           0 ≤ x ≤ 1       y = 2 - x 2 ;         1 ≤ x ≤ 2

b )

J = 3 ln ⁡ 3 - 2 π 8

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}