Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 421234567891011121314151617181920212223242526272829303132333435363738394041434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 1: Calcule a integral dupla da função e - x 2 + y 2 no disco unitário centrado na origem.

Passo 1

Começaremos aqui sabendo exatamente com quem estamos lidando e para isso, nada melhor que conhecer a região de integração.

Como próprio enunciado disse:

“disco unitário centrado na origem”

Então a integral a se resolver é essa daqui oh:

∬ D   e - x 2 + y 2   d A

Passo 2

Bem, se vamos trabalhar com uma região circular e, além disso, a integral que vamos fazer envolve x e y ao quadrado, então é muito legal pensarmos em uma mudança para coordenadas polares ;)

x = r cos ⁡ θ

y = r sin ⁡ θ

Uma equação que ajuda aqui é a equação do disco:

x 2 + y 2 = r 2

E não se pode esquecer-se do Jacobiano, que nesse caso é

J = r

Passo 3

Bem, mas essa mudança só termina quando a gente encontra a variação de θ e r na nossa região:

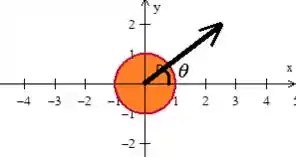
Veja que o ângulo θ nessa mudança sempre varia saindo do eixo x girando no sentido anti-horário, logo, para termos um disquinho completo, θ tem que girar uma volta inteira...

0 ≤ θ ≤ 2 π

Enquanto o r varia da origem até o raio máximo que é um no caso, já que o círculo é unitário...

0 ≤ r ≤ 1

Passo 4

Voltando para a integral que queremos resolver...

∬ D   e - x 2 + y 2   d A

Substituindo tudo o que encontramos nos passos anteriores...

∬ D   e - x 2 + y 2   d A = ∫ 0 2 π ∫ 0 1 e - r 2 ⋅ J   d r d θ =

Veja que não se pode esquecer-se de multiplicar a função pelo jacobiano...

∫ 0 2 π ∫ 0 1 e - r 2 r   d r d θ

Bora calcular essa integral aí?

Passo 5

Calculando a integral de dentro fazendo uma substituição...

∫ 0 2 π ∫ 0 1 e - r 2 r   d r d θ ;

Onde podemos trocar o termo - r 2 = t onde...

d t = - 2 r d r         o u         r d r = - d t 2

Trocando também os limites de integração (cuidado para não esquecer-se disso, heim):

r = 0           →                 t = 0

r = 1           →                 t = - r 2 = - 1

Logo...

∫ 0 2 π ∫ 0 1 e - r 2 r   d r d θ = ∫ 0 2 π ∫ 0 - 1 e t - d t 2 d θ =

∫ 0 2 π ∫ - 1 0 e t d t 2 d θ =

∫ 0 2 π e t 2 - 1 0 d θ = ∫ 0 2 π 1 2 - e - 1 2 d θ =

Como o termo dos colchetes é uma constante, pode vasar da integral...

1 2 - e - 1 2 ∫ 0 2 π d θ = 1 2 - e - 1 2 2 π =

1 - e - 1 π

Resposta

1 - e - 1 π

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}