UFABC. Cálculo. Funções de Várias Variáveis. Lista 6 - Integrais Duplas. Questão 7g.
7 - Usando coordenadas polares, calcule:
g) , onde é a região limitada por . Interprete o resultado geometricamente.
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nessa questão, temos que calcular a integral dupla de limitada por uma região onde .
Organizando essa equação vemos que se trata da equação de uma elipse
Quando estamos tratando de uma elipse em , podemos converter as coordenadas para as coordenadas , ou seja, para as coordenadas polares.
Como temos uma elipse, a conversão para polares é um pouco diferente. Primeiro, quando vamos converter , temos que adicionar um termo , então . Para temos que fazer a mesma coisa porem com outro valor, .
Ok, mas de onde saiu esses e ?? 🤔
A equação da elipse é
Correto?
É daqui que tiramos os valores de e !
Passo 2
Antes de montar nossa integral, vamos ver como é nossa região de integração?
Se plotarmos , vamos obter
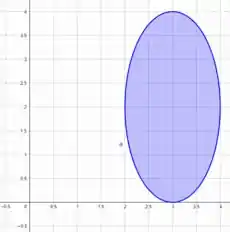
Perceba que nossa elipse está com seu centro um pouco distante da origem do nosso sistema.
Dessa forma fica muito difícil obter os valores de integração para e , não acha?
Então o que podemos fazer??
Podemos transladar nossa origem para o centro da nossa região, não é?
Com isso, temos que fazer a seguinte mudança. Lembrando que nosso e
Dessa forma podemos obter nosso substituindo isso na nossa equação
Dividindo nossa equação por e colocando em evidencia, temos
Se , então
Assim, nossos limites de integração em vai de a .
Passo 3
Como agora estamos no centro da nossa elipse, a variação do ângulo percorre todos os valores trigonométricos, logo, os limites de integração para é de a .
E o jacobiano? O que muda nele?
O jacobiano continua o mesmo quando temos uma elipse , se e , então
Agora temos todos os dados pra montar nossa integral!
Primeiro integrando a , aplicamos o método de integração de polinômios: dividimos a variável pela sua potencia e somamos no seu expoente.
Aplicando os limites de integração
Tranquilo até aqui?
Passo 4
Agora com esse resultado, integramos com relação a .
Como temos apenas uma constante, sabemos que a integral de uma constante é a própria constante multiplicada pela integral, correto?
Aplicando os limites de integração, temos
Acabou? Ainda não!
No fim do enunciado, foi pedido para interpretarmos o resultado a partir de uma perspectiva geométrica.
E o que podemos afirmar é que a area dentro da região limitada por é de .
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
