Considere a região do plano limitado pela curva
- Esboce em coordenadas cartesianas e polares.
- Calcule
Passo 1
- Bom, pra começar essa letra (a) aí, bora começar completando o quadrado.
Com a função escrita desse jeito fica mais fácil da gente ver que se trata de uma circunferência deslocada no eixo y. Seu centro passa a ser no ponto (0,1), e tem raio 1.
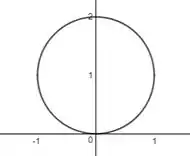
Agora passando tudo isso pra coordenadas polars, as substituições são
Bora lembrar como a gente estuda a variação dos intervalos?
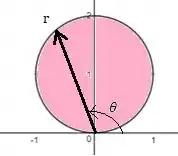
Observando o gráfico vemos que nosso varia de 0 a , uma vez que zero representa o a partida do eixo x positivo, fazendo uma “varredura” de meia volta () até o eixo x negativo.
Para obtermos a variação do r, basta fazer as devidas substituições.
Com isso observamos que o raio varia entre 0 e ().
Passo 2
- Agora calculando ficamos com
Resposta
Exercícios de Livros Relacionados
Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}