Coordenadas polares
Calcule , em que é a região do primeiro quadrante limitada pelo círculo . Esboce a região .
Passo 1
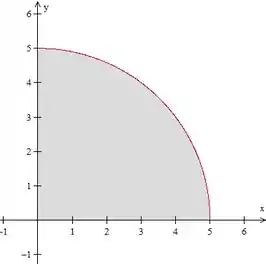
Vamos começar esboçando a região de integração, temos um círculo de raio centrado na origem limitado ao primeiro quadrante:
Passo 2
Beleza, agora vamos escrever matematicamente essa região. Como temos um círculo, vamos usar coordenadas polares:
A região para a ser então (pois temos um quarto de volta trigonométrica) e , pois o raio varia desde a origem até a circunferência de raio .
Passo 3
Fazendo essa substituição na integral, temos:
Passo 4
Integrando em relação a , temos:
Agora em relação a :
Resposta
Exercícios de Livros Relacionados
Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}