Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 441234567891011121314151617181920212223242526272829303132333435363738394041424345464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 3: Calcule

∬ D   ln ⁡ x 2 + y 2   d A

Onde D é a região do primeiro quadrante entre as circunferências x 2 + y 2 = 1 e x 2 + y 2 = 4 .

Passo 1

Bem, a nossa primeira tarefa para resolver uma integral dupla como essa é definitivamente entender a região de integração. O que, para a nossa alegria, a região D é uma região entre as circunferências e está apenas no primeiro quadrante, então a gente pode desenhar colocando isso no papel:

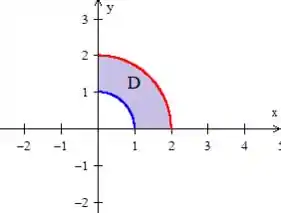
Viu só?

Passo 2

Como estamos trabalhando com uma região circular, podemos usar as famosas coordenadas polares onde vamos trocar:

x = r cos ⁡ θ

y = r sin ⁡ θ

O Jacobiano dessa mudança é um cara especial que, caso você não se recorde...

J = r

Outra equação vinda da soma quadrática dessas coordenadas é a equação do círculo:

x 2 + y 2 = r 2

SHOW! Mudança de coordenadas feitas, vamos para a nossa segunda tarefa: encontrar a variação das novas coordenadas r e θ dentro da nossa região D . Partiu?

Passo 3

Para encontrar tais variações, sempre é interessante colocar como as variações acontecem nas coordenadas polares em cima da nossa região:

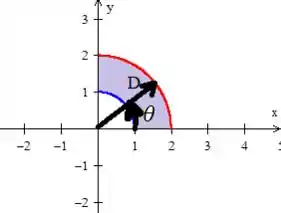
Veja que o raio r é o cara que para formar D , começa a variar na circunferência de raio 1 e sai na segunda de raio 2 :

1 ≤ r ≤ 2

Quanto ao ângulo θ , veja que ele está saindo de 0 ° e indo até 90 ° ...

0 ≤ θ ≤ π 2

Passo 4

Voltando então para a integral que temos que fazer, e substituindo tudo, não se esquecendo de multiplicar a função pelo Jacobiano...

∬ D   ln ⁡ x 2 + y 2   d A = ∫ 0 π 2 ∫ 1 2 ln ⁡ r 2 ⋅ J   d r d θ =

∫ 0 π 2 ∫ 1 2 ln ⁡ r 2 ⋅ r   d r d θ

A integral está montada, agora é só correr para o abraço e calcular mesmo!

Passo 5

∫ 0 π 2 ∫ 1 2 ln ⁡ r 2 ⋅ r   d r d θ = ∫ 0 π 2 ∫ 1 2 ln ⁡ r 2 ⋅ r   d r d θ

Podemos calcular essa integral de dentro

∫     ln ⁡ r 2 ⋅ r   d r

Fazendo uma integração por partes, onde vamos considerar o l n como sendo a função que deve ser derivada u enquanto o d v = r d r ...

u = ln ⁡ r 2             →                       d u = 1 r 2 ⋅ 2 r   d r = 2 r d r

d v = r   d r                               →                                     v = r 2 2                                                      

Pela fórmula de integração por partes:

∫ u   d v = u ⋅ v - ∫ v   d u         →

∫     ln ⁡ r 2 ⋅ r   d r = ln ⁡ r 2 ⋅ r 2 2 - ∫ r 2 2 ⋅ 2 r d r         →

∫     ln ⁡ r 2 ⋅ r   d r = ln ⁡ r 2 ⋅ r 2 2 - ∫ r d r         →

∫     ln ⁡ r 2 ⋅ r   d r = r 2 2 ln ⁡ r 2 - r 2 2

Logo...

∫ 0 π 2 ∫ 1 2 ln ⁡ r 2 ⋅ r   d r d θ = ∫ 0 π 2 r 2 2 ln ⁡ r 2 - r 2 2 1 2 d θ =

∫ 0 π 2 2 2 2 ln ⁡ 2 2 - 2 2 2 - 1 2 ln ⁡ 1 - 1 2 d θ     →

∫ 0 π 2 2 ln ⁡ 4 - 2 - 1 2 ln ⁡ 1 + 1 2 d θ = ∫ 0 π 2 2 ln ⁡ 4 - 3 2 d θ

2 ln ⁡ 4 - 3 2 ∫ 0 π 2 d θ = 2 ln ⁡ 4 - 3 2 ⋅ π 2 =

π ln ⁡ 4 - 3 π 4

Resposta

π ln ⁡ 4 - 3 π 4

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}