Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 791234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677788081828384858687888990919293949596979899100

Enunciado

Origem do Exercício

Mude a integral cartesiana para uma integral polar equivalente e calcule a integral polar de:

∫ - 1 1 ∫ 0 1 - x 2 d y d x

  1. π / 2
  2. π
  3. 3
  4. π 2 + 3
  5. 1 / 2

Passo 1

Essa integral é bastante simples: só precisamos “converter” duas coisas (1) os limites de integração e (2) os diferenciais d y   d x .

Começamos pelos limites de integração. Os originais eram:

- 1 ≤ x ≤ 1

0 ≤ y ≤ 1 - x 2

Desenhar a região é sempre uma ótima ideia, quase sempre você consegue determinar os novos limites de integração só olhando o desenho.

É importante saber que a função 1 - x 2 dá a metade superior de uma circunferência de raio 1 ! A partir daí, os outros limites são constantes, e fica fácil fazer o desenho:

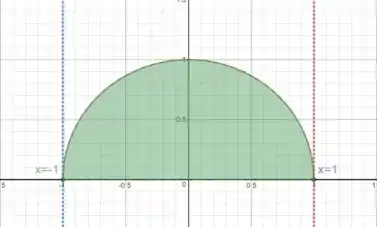
Passo 2

Agora, olhando para o desenho, vamos definir os intervalos em que vamos integrar r e θ .

Como temos um círculo de raio 1 :

0 ≤ r ≤ 1

E como estamos integrando a metade superior do círculo:

0 ≤ θ ≤ π

Se estivéssemos integrando o círculo inteiro, por exemplo, θ teria que variar de 0 até 2 π .

Passo 3

Depois disso, precisamos lembrar do jacobiano para coordenadas polares, e então podemos converter os diferenciais:

d x   d y = r   d r   d θ

E agora já podemos substituir tudo na integral:

∫ - 1 1 ∫ 0 1 - x 2 d y d x = ∫ 0 π ∫ 0 1 r   d r   d θ

Ok, terminamos a conversão, agora vamos calcular a integral.

Passo 4

Primeiro integramos em relação a r , lembrando que:

∫ r   d r = r 2 2 + C

Então:

∫ 0 π ∫ 0 1 r   d r   d θ = ∫ 0 π 1 2 2 - 0 2 2   d θ = 1 2 ∫ 0 π d θ

Agora integramos em relação a θ , lembrando que:

∫ d θ = θ + C

Então:

1 2 ∫ 0 π d θ = 1 2 π - 0 = π 2

Resposta

Letra (a).

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}