UNICAMP – Cálculo 2 – 2020.2 – P1 – Discursiva
Calcule a integral
onde a região é definida por .
Passo 1
Desenhando tudo o que o enunciado nos dar temos:
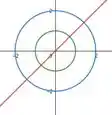
Porém a área que estamos interessados é a área abaixo da reta (reta vermelha), fora do círculo de raio (círculo verde), dentro do círculo de raio (círculo azul) e no primeiro quadrante.
Sabendo disso vamos usar coordenadas polares para resolver essa questão.
Passo 2
Primeiro vamos passar o que temos para polar. Sabemos que:
Em coordenadas polares:
Sabemos que vai de até a reta , ou seja:
Então:
Agora é só resolver a integral dupla!
Passo 3
Resolvendo a integral:
Resposta
Exercícios de Livros Relacionados
Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}