UFSC, Araranguá, Cálculo B, P3 - 2022.2, Questão 4
Determine o volume do sólido limitado pelas superfícies , e
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu três superfícies e pediu pra gente calcular o volume entre elas. O nosso sólido está acima do plano , , abaixo do cone e dentro do cilindro .
O nosso sólido também está acima do disco , no plano , cujo limite tem a equação .
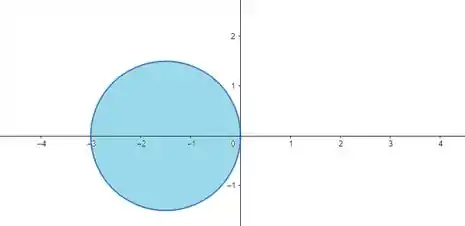
Em coordenadas polares, nós temos e . Substituindo isso na nossa equação , temos:
Portanto, o disco é dado por:
Nós temos um teorema que diz que se nós temos uma função contínua em uma região polar como essa, então podemos escrever a integral:
Nós já encontramos nossos intervalos de integração, então o que nós vamos fazer é escrever nossa função em coordenadas polares e calcular nossa integral pra encontrar o volume do sólido.
Então, vamos lá!
Passo 2
Vamos montar nossa integral. Como , em coordenadas polares temos . Assim,
Vamos integrar primeiro em relação a :
Aplicando os limites em :
Passo 3
Galera, pra calcular nossa integral em relação a , vamos primeiro usar a identidade trigonométrica:
Substituindo na integral:
Na primeira integral, nós temos:
Pra resolver a segunda integral, nós vamos precisar fazer uma substituição. Vamos chamar:
Substituindo em , temos:
Voltando pra nossa integral original e substituindo os intervalos de integração, temos:
E encontramos nosso volume.
Valeu, galera! 😉