Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 251234567891011121314151617181920212223242627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Calcule a integral dupla

∬ R x + 1 d A

Onde R é a região definida por

R = x , y 2 y ≤ x 2 + y 2 ≤ 4 y ,   - y ≤ x ≤ y

Passo 1

Bem, primeiro de tudo, vamos tentar entender nossa região.

Nós temos a fronteira de:

x 2 + y 2 ≤ 4 y

⇒ x 2 + y 2 - 4 y = 0

⇒ x 2 + y - 2 2 = 4

Uma circunferência com centro em 0,2 de raio 2 .

Mas também temos que pegar a região externa de.

2 y ≤ x 2 + y 2

⇒ 0 = x 2 + y 2 - 2 y

⇒ x 2 + y - 1 2 = 1

Também uma circunferência descentralizada, mas dessa vez em 0,1 e com raio 1 .

E por fim, temos duas retas:

- y = x         e         x = y

Se desenharmos, vamos ter:

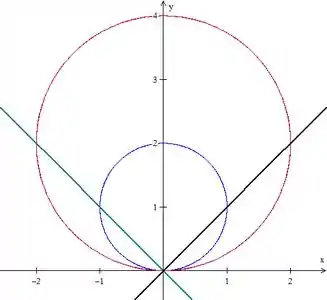
Aquele x 2 + y 2 já nos dava uma dica que temos que usar coordenadas polares, mas com o desenho da pra ver que o θ também é bem definido, então vamos ver como que fica!

Passo 2

Vamo lembrar como são as coordenadas polares:

x = r cos ⁡ θ

y = r sen ⁡ θ

J = r

E nossa região vai ficar:

2 y ≤ x 2 + y 2 ≤ 4 y → 2   r sen ⁡ θ ≤ r 2 ≤ 4   r sen ⁡ θ

⇒ 2 sen ⁡ θ ≤ r ≤ 4 sen ⁡ θ

E as retas nos dão:

- y = x → - r sen ⁡ θ = r cos ⁡ θ

⇒ - sen ⁡ θ = cos ⁡ θ → θ = 3 π 4

E

x = y → r cos ⁡ θ = r sen ⁡ θ

cos ⁡ θ = sen ⁡ θ → θ = π 4

Então podemos escrever nossa integral:

∬ R x + 1 d A = ∫ π 4 3 π 4 ∫ 2 sen ⁡ θ 4 sen ⁡ θ r cos ⁡ θ + 1 r   d r d θ

Nada muito complicado, é só partir pro abraço!

Passo 3

Vamos resolver:

∫ π 4 3 π 4 ∫ 2 sen ⁡ θ 4 sen ⁡ θ r cos ⁡ θ + 1 r   d r d θ = ∫ π 4 3 π 4 ∫ 2 sen ⁡ θ 4 sen ⁡ θ r 2 cos ⁡ θ + r   d r d θ

⇒ ∫ π 4 3 π 4 r 3 3 cos ⁡ θ + r 2 2 │ 2 sen ⁡ θ 4 sen ⁡ θ   d θ

= ∫ π 4 3 π 4 64 sen 3 ⁡ θ - 8 sen 3 ⁡ θ 3 cos ⁡ θ + 16 sen 2 ⁡ θ - 4 sen 2 ⁡ θ 2   d θ

⇒ ∫ π 4 3 π 4 56 sen 3 ⁡ θ 3 cos ⁡ θ d θ + ∫ π 4 3 π 4 12 sen 2 ⁡ θ 2   d θ

Vamos só separar aqui pra não ficar muito confuso...

Passo 4

Primeiro temos:

∫ π 4 3 π 4 56 sen 3 ⁡ θ 3 cos ⁡ θ d θ

Podemos fazer a substituição:

u = sen ⁡ θ

d u = cos ⁡ θ d θ

Então, vamos ter:

∫ 56 sen 3 ⁡ θ 3 cos ⁡ θ d θ = 8 3 ∫ u 3 d u = 56 3 ∙ u 4 4 = 14 sen ⁡ θ 4 3

Aplicando os limites de integração:

14 sen 4 ⁡ θ 3 │ π 4 3 π 4 = 14 3 sen ⁡ 3 π 4 4 - sen ⁡ π 4 4 = 14 3 2 2 4 - 2 2 4 = 0

Isso tudo pra dar zero?? Mas calma que ainda tem o outro pedaço, vamos ver!

Passo 5

O outro pedaço era:

∫ π 4 3 π 4 12 sen 2 ⁡ θ 2   d θ

Vamos lembrar que sen 2 ⁡ θ = 1 - cos ⁡ 2 θ 2 , então:

∫ π 4 3 π 4 6 sen 2 ⁡ θ   d θ = ∫ π 4 3 π 4 6 1 - cos ⁡ 2 θ 2   d θ

⇒ 3 ∫ π 4 3 π 4 1 - cos ⁡ 2 θ   d θ = 3 θ │ π 4 3 π 4 - sen ⁡ 2 θ 2 │ π 4 3 π 4 = 3 2 π 4 - - 1 - 1 2 = 3 π 2 + 3

Como o primeiro pedaço deu zero, então a resposta vai ser essa mesmo!

Resposta

3 π 2 + 3

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}