USP– Cálculo 1 – Lista 1 – Questão 5.7
Uma lâmpada esta acesa no solo a de um edifício. Um homem de de altura anda a partir da luz em direção ao edifício a . Determine a velocidade com que o comprimento de sua sombra sobre o edifício diminui quando ele está a do edifício e quando ele está a do edifício.
Passo 1
Oi pessoal, tudo bem por aí? Essa é uma questão de taxas relacionadas, vamos ver o que o problema nos diz! Ela nos diz que temos uma pessoa andando em direção a um prédio. Em um dado momento temos a velocidade de aproximação e a posição da pessoa. E pediu a taxa de variação da altura da sombra em relação ao tempo. E agora, como relacionar?
Mas espera aí! Sabemos a relação de proporcionalidade entre os tamanhos! Dá uma olhada nesse esquema aqui
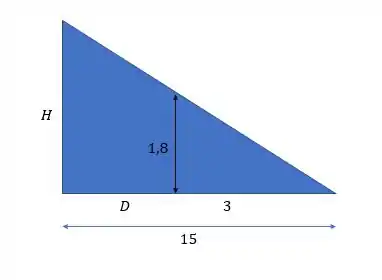
No nosso caso ele quer o tamanho da sombra quando a pessoa está a metros da luz, e depois a . No esquema está apenas a primeira situação. Por proporcionalidade
Então vamos derivar dos dois lados em relação ao tempo e substituir nos dados!
Tranquilo? Relaxa, vou fazer passo a passo contigo!
Bora lá!
Passo 2
Derivando a relação temos
Agora vamos os dados:
Assim
E substituindo por temos
E é isso! Até a próxima!