Um fabricante produz por semana toneladas de um certo produto. O preço de venda é de unidades monetárias por tonelada do produto e está relacionada com por , . O custo de produção é de unidades monetárias. Determine para que o lucro seja máximo. Determine, também, o lucro máximo.
Passo 1
Bom, para determinarmos que maximiza o lucro, precisamos derivar a função que representa o lucro e encontrar seu ponto de máximo. Sabemos que o lucro é igual ao valor vendido menos o custo de produção. Possuímos apenas a equação do custo, mas a partir da relação
podemos encontrar a função que representa o valor da venda de toneladas do produto. Primeiro, temos que isolar , que representa o preço por tonelada.
Para saber o valor arrecadado na venda de toneladas precisamos multiplicar o valor por .
Finalmente, podemos determinar a função que representa o lucro, subtraindo a função da venda pela função do custo.
Passo 2
Chegamos na parte mais importante do exercício. Temos que achar o máximo da função . Então, primeiro, vamos derivar a função.
Agora que temos a derivada , podemos encontrar os pontos críticos fazendo
Passo 3
Finalmente, podemos fazer o teste da primeira derivada, analisando o sinal da derivada perto de para verificar se é um ponto de máximo.
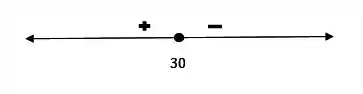
Então, como a derivada muda de positiva para negativa em , podemos afirmar que esse é um ponto de máximo da função
Passo 4
O valor do lucro máximo é obtido substituindo na função .