UFRJ – Cálculo 1 – Lista 13 – Questão 8
Uma cerca de de altura está situada a uma distância de da parede lateral de um galpão. Qual o comprimento da menor escada cujas extremidades se apoiam na parede e no chão do lado de fora da cerca?
Passo 1
Incialmente, podemos fazer uma ilustração do que está acontecendo. Supondo uma distância da extremidade da escada até a parede e uma altura :
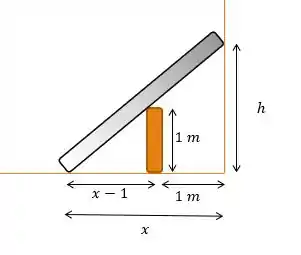
Repare que o triangulo retângulo de catetos e é semelhante ao triangulo de catetos e . Assim,
Logo,
Como queremos minimizar o comprimento da escada então vamos aplicar o Teorema de Pitágoras para achar seu comprimento.
Usando a relação :
Passo 2
Agora que já temos uma equação para o comprimento da escada vamos minimiza-la. Repare que para minimizar basta minimizarmos o que está dentro da raiz. Assim,
Agora não tem segredo, vamos derivar e igualar a zero para encontrar os pontos críticos.
Pela regra do quociente:
Logo,
Igualando a zero:
Repare que , pois o denominador não pode ser zero.
Como :
Portanto,
Passo 3
Para acharmos o comprimento da escada, basta voltarmos para equação do passo 1:
Fazendo :
Fazendo as contas: