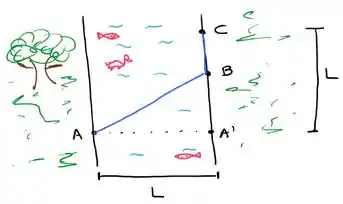
Uma pessoa no ponto da margem de um rio tem que atravessá-lo para chegar ao ponto da margem oposta (vide figura abaixo). A largura do rio é e a distância ao longo do rio entre os pontos (obtido atravessando o rio perpendicularmente à sua margem) e também é .
A figura abaixo mostra um possível caminho para isso, onde a pessoa sai do rio no ponto .
A velocidade da pessoa em terra é e na água é . Você pode, se quiser, trabalhar nas unidades em que e . Determine a distância de a para que o tempo gasto seja mínimo.
Passo 1
Bom, ignorando o fato que o responsável por esse desenho da prova tem um talento artístico nato, a gente precisa achar uma expressão para o tempo total em função da distância , e aí poderemos derivar e igualar esse cara a para otimizar a função. O tempo total é dado pelo tempo percorrido em água mais o tempo percorrido em terra, ou seja:
Ora, a gente sabe que uma velocidade constante equivale a velocidade média, assim vamos ter
E
Como queremos o tempo, vamos escrever essas duas expressões assim
Opa, mas ele disse que a velocidade na água é e a na terra é , assim vamos ter
Como ele deu o valor de que podemos usar, vamos usar né para facilitar nossa vida.
Agora falta achar essas duas distâncias.
A distância que a pessoa caminha na terra vale o segmento , ou seja, . Assim temos
Já a em água valerá a hipotenusa do triângulo retângulo de catetos que é e os catetos são
E
Por Pitágoras vamos ter
Isso nos diz que
Enfim, o tempo em função de é dado da seguinte forma:
Vamos trocar por também como ele sugeriu ali em cima.
Dando uma última arrumação
Enfim, essa é a função que queremos otimizar!
Passo 2
Vamos derivar esse tempo e igualar a :
Assim vamos ter
Qual desses dois que vão servir para a gente? Repara que o segundo é maior que o valor de que é , como é necessariamente menor que temos
E esse é o valor de que otimiza o menor tempo de travessia do ponto até .