Uma refinaria de petróleo está em A na margem norte de um rio reto que tem de largura. Um oleoduto deve ser construído da refinaria até um tanque de armazenamento em B na margem sul do rio, a leste da refinaria. O custo de construção do oleoduto é sobre a terra, até um ponto P na margem norte do rio e sob o rio até o tanque.
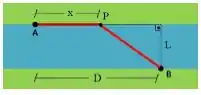
- Obtenha o custo total de construção do oleoduto, , em função da distância , entre A e P.
- Determine os pontos críticos de em .
- Qual o valor de que minimiza o custo de construção do oleoduto?
Passo 1
Fala aí, pessoal, vamos fazer uma questão bem prática que é uma questão de custos de um projeto!
Começamos com a distância entre os pontos A e P que fica sobre a terra, o preço por quilômetro é . Então o custo de instalar todo esse comprimento é:
Agora vamos calcular a distância na água entre os pontos P e B:
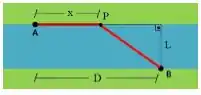
Veja que temos a largura do rio e o comprimento do rio , você concorda comigo que formamos um triângulo nessa região do rio:
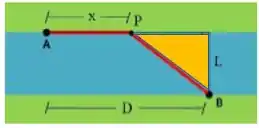
Vamos olhar com mais carinho para o triângulo:
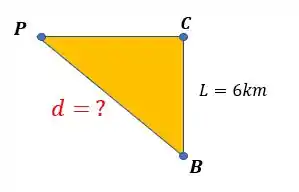
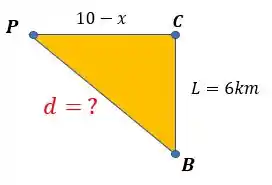
Nós queremos saber a distância que o oleoduto vai passar pela água, então queremos descobrir o valor de . Beleza? Veja que temos um triângulo retângulo, então podemos usar o Teorema de Pitágoras, mas para isso, precisamos saber o valor do outro cateto entre os pontos P e C.
Se olharmos que o comprimento total da margem é , se a distância entre e é igual a , então a distância entre e é o valor total da margem menos a distância :
Então terminamos de formar nosso triângulo:
Passo 2
Nossa distância sobre a água então é:
Então o custo desse trecho é:
Então o custo total é a soma do custo do trecho sobre terra e do trecho sob o rio:
Melhorando esse formato ai:
Essa é a função do nosso custo! Já foi a letra “a”, certo?
Passo 3
Agora vamos para a letra “b”, ele deseja saber quais são os pontos críticos para essa função de custo:
Vamos relembrar que os pontos críticos existem quando encontramos um ponto onde a derivada da função não existe ou um ponto onde a derivada da função é igual a zero. Então o nosso primeiro passo é calcular a derivada dessa função de custo:
Veja que podemos reescrever essa raíz quadrada como:
Derivando essas parcelas, vamos usar a Regra da Cadeia:
Simplificando isso aí:
Agora que sabemos a derivada da função, queremos saber onde ela não existe ou onde ela é igual a zero. Vamos começar pensando que valores de fazem com que essa função não exista, ela não existirá, caso o denominador seja igual a zero:
Vamos elevar ao quadrado esses dois lados:
Se nós desenvolvermos esse produto notável:
Usando Bhaskara, vamos encontrar:
Como temos uma raíz quadrada de um valor negativo, teremos duas raízes do polinômio como números complexos, logo, essas raízes não estão dentro do intervalo .
Não temos pontos críticos através da inexistência da derivada, então vamos tentar encontrar pontos onde a derivada é igual a zero:
Vamos passar o denominador para o outro lado:
Vamos colocar essa primeira parcela dentro da raiz quadrada em evidência:
Podemos retirar ela de dentro da raiz quadrada:
Como:
Então podemos cortar esse elemento das duas parcelas:
Vamos passar todos os números para o outro lado:
E como vamos terminar de resolver isso? Elevar os dois lados ao quadrado:
Então:
Olhando bem para essa igualdade:
Chegamos em uma igualdade nos denominadores:
Então temos que resolver através de Bhaskara:
Então temos as seguintes raízes possíveis:
Lembrando que nosso intervalo é de a , então a única raiz que podemos usar como ponto crítico é:
Logo, chegamos a conclusão que esse é o único ponto crítico!
Passo 4
Agora que já encontramos o valor do ponto crítico, nossa letra “c” nos pede o valor de que minimiza o custo de construção do oleoduto, ou seja, o ponto mínimo da função de custo:
Mas para encontrar esse ponto mínimo, temos que usar o ponto crítico que encontramos no item anterior! Agora você já viu sentido no que estamos fazendo? Beleza!
E como nós verificamos se esse ponto é mínimo? Através do teste da primeira derivada, se:
E
Ai sim podemos afirmar que é ponto de mínimo!
Então vamos testar isso na derivada:
Para um ponto maior que o ponto crítico:
Calculando isso:
Agora vamos calcular para um ponto menor que o ponto crítico:
Então:
Como o teste da primeira derivada bateu com o que pensamos inicialmente:
E
Sabemos que é um ponto que minimiza o custo!