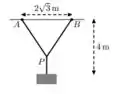
- Um peso deve ficar suspenso a 4m de uma superfície horizontal por meio de uma armação de arame em forma de Y, como na figura abaixo (os pontos A, B e P são os vértices de um triângulo isósceles). Se os pontos de sustentação A e B distam m, determine o comprimento mínimo de arame necessário.
Passo 1
Olá, galerinhaa!!! Vamos lá? Aqui nesta questão, vamos tratar de um problema de otimização.
Mas o que é otimizar?
Bom, otimizar significa chegar ao ótimo, à melhor situação possível. Em Cálculo 1 isso implica dizer que vamos ter uma situação que pode ser descrita por uma função , e vamos procurar um , de tal forma que
Esse ponto representa o cenário ideal que buscamos alcançar.
Ah, e mais uma coisa antes de passarmos pra questão em si, otimizar pode tanto significar obter o máximo quanto o mínimo de uma situação. Agora vamos pra nossa questão.
Passo 2
Vamos agora observar a seguinte imagem
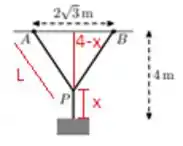
A partir dela nós podemos escrever uma expressão para a nossa quantidade de arame (lembrando que )
Essa ainda não é uma expressão boa para nós, pois ela tem duas variáveis, L e x.
Passo 3
Vamos agora tentar deixar em função de uma variável só, no caso vamos escolher deixar em função de x.
Se observarmos bem, dentro do triângulo isósceles formado por A, B e P, podemos achar o seguinte triângulo.
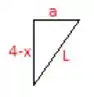
Como o é isósceles, o lado a tem metade da distância de A para B, logo . E,
Substituindo esse valor na expressão de temos,
Passo 4
Agora, vamos derivar nossa função. Assim,
Agora, igualamos nossa derivada a zero e
E, se escolhermos o menor valor para x, que é , temos
Logo, a menor quantidade de arame que pode ser usada é 7 metros..
Ufaa, que questão trabalhosa, mas enfim, terminamos 😅😅. Até a próximaa!!
Resposta