4. Um determinado produto tem um preço de custo de por unidade, e ao vender o produto por , é possível vender . Além disso, a cada centavo descontado no preço, é possivel aumentar a venda em . Reciprocamente, ao aumentarmos em um centavo o preço de venda, deixamos de vender . Que preço deve ser cobrado no produto, para que o lucro obtido seja máximo?
Passo 1
Oi, galerinha! Tudo bom? Aqui, nós temos uma questão de otimização, onde queremos encontrar o lucro máximo que podemos ter com essas vendas.
De um modo geral, podemos dizer que o lucro será dado pela quantidade de peças vendidas multiplicada pelo preço de venda, descontado do preço de custo. Transformando em fórmula fica assim:
Vamos considerar tudo em centavos para facilitar os cálculos, e colocar algumas informações já fornecidas pelo problema nessa fórmula!
Vamos considerar
E temos que o custo fornecido pelo enunciado é
Logo o nosso lucro fica assim
Para substituir a quantidade vendida nessa formula, precisamos de atenção!
Passo 2
Repara que o enunciado diz o valor é de para . Porém se pode ser dado um desconto de a cada a mais. Deste modo, podemos dizer que a quantidade vendida será
Lembrando que é o nosso .
Passo 3
Juntando tudo na nossa função de lucro , ficamos com
Reescrevendo:
Mas repara que essa função tem que ser limitada, pois se cobramos um valor menor que o valor de custo () teremos prejuízo. Assim como, se cobramos um valor muito alto não venderemos nenhuma unidade. Como a função lucro é uma função do segundo grau, podemos calcular as raízes com a fórmula de Baskhara, e encontraremos que esse valor máxmo é de . Portanto, temos:
Agora vamos achar o máximo global neste intervalo de , visando encontrar o lucro máximo.
Passo 4
Primeiramente vamos achar os pontos críticos! Fazemos isso, derivando a nossa função e igualando a zero.
Derivando,
Igualando a zero,
Resolvendo essa equação temos que
Mas ainda não sabemos se este é um ponto de máximo ou de mínimo. Nós vamos descobrir isso, comparando com outros pontos conhecidos!
Passo 5
Pela fórmula do lucro e como discutido no Passo 3, temos que
Pois com esses preços não teríamos lucro.
Agora vamos substituir na fórmula do lucro e se encontramos uma valor maior que zero, temos que esse será o valor máximo, ou seja, o lucro máximo
Como o valor é maior que zero, temos que esse é um ponto de máximo! Como essa função é de segundo grau, já poderíamos desconfiar disso, pois ela é uma parábola aberta pra baixo. Mas fazendo essa comparação, você consegue descobrir mesmo no caso de funções que você não conhece a geometria.
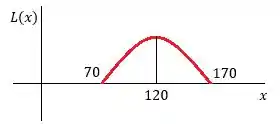
Então, para máximar o lucro, o preço a ser cobrado será de . Passando para reais ficamos com .