Constrói-se uma janela normanda colocando-se um semicírculo em cima de uma janela retangular. Encontre as dimensões da janela de área máxima, sabendo-se que seu perímetro é de .
Passo 1
Observe a figura abaixo, que representa a situação descrita no enunciado.
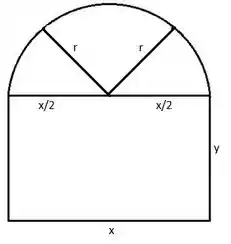
Para achar a área máxima total, vamos dividir a figura em duas áreas diferentes e depois soma-las. A primeira é a área do retângulo, dada por
A outra é a área do semicírculo, dada por
Observe, pela figura, que
Logo,
Portanto, a área total, que deve ser otimizada é
Passo 2
Precisamos de uma relação entre as variáveis. Nesse caso, é fácil obter essa relação, visto que o enunciado diz que o perímetro vale . Então
Substituindo o por :
Agora podemos isolar uma das variáveis. Escolhi isolar .
Passo 3
Já podemos substituir na equação da área total.
Passo 4
E finalmente vamos derivar para encontrar seu ponto de máximo.
Passo 5
Tendo a derivada, podemos encontrar os pontos críticos, igualando-a a zero.
Agora temos que descobrir se o ponto encontrado é uma máximo da função. Analisando o sinal da derivada perto de temos que
- Antes de:
- Depois de:
Logo, é um ponto de máximo local.
Passo 6
Também precisamos do valor de quando . Sabemos que
e substituindo o encontramos