USP– Cálculo 1 – Lista 1 – Questão 5.4
A partícula A se move ao longo do semieixo positivo e a partícula B move-se ao longo do gráfico da função . Num certo instante, a partícula A está no ponto (5, 0) e afasta-se da origem com velocidade unidades por segundo e a distância de B até a origem e unidades, afastando-se da origem com velocidade unidades por segundo. Qual a taxa de variação da distância entre A e B nesse instante?
Passo 1
Oi pessoal, tudo bem por aí? Essa é uma questão de taxas relacionadas, vamos ver o que o problema nos diz! Ela nos diz que temos dois pontos A e B. A partícula A está no ponto no eixo e se afasta da origem. O ponto B está em cima da parte negativa da reta .
Ele diz qual é a distância das partículas até a origem e dá as velocidades de afastamento. E nos pede qual a taxa com que a distância entre eles está aumentando.
E agora, como relacionar?
Mas espera aí! Vamos colocar isso tudo em um gráfico!
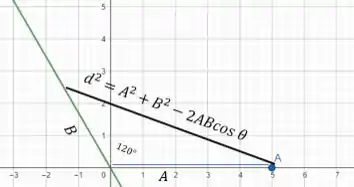
em verde temos a reta, ali temos a distância . Já o A está no eixo e está representado em azul. Por trigonometria temos o ângulo entre os lados A e B e a distância entre esses pontos é dada pela lei dos cossenos! Agora é só derivar tudo em relação ao tempo e substituir os valores!
Tranquilo? Relaxa, vou fazer passo a passo contigo!
Bora lá!
Passo 2
Derivando a fórmula da distância entre as partículas
Lembrando que é constante!
Agora vamos os dados:
Quando e
As velocidades
Assim
E é isso! Até a próxima!