USP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - USP - Lista 1, Questão 7.30
Determine o cone circular reto de maior volume que pode ser inscrito numa esfera de raio .
Passo 1
Faaaala galerinha, tudo bem com vocês?
Nessa questão temos um problema de otimização. Basicamente, temos uma esfera de raio e queremos inscrever um cone circular reto dentro dela, de modo que ele tenha o maior volume possível.
Vocês lembram qual a expressão que determina o volume de um cone circular reto? Bora revisar:
onde é o raio da base do cone e a sua altura.
Queremos que essa expressão seja máxima, então a ideia é a mesma de todos os problemas otimização: derivamos e igualamos a zero.
A grande dificuldade é que temos duas variáveis nessa função, e precisamos derivá-la apenas em relação a uma das duas.
Assim, vamos usar o fato do cone estar inscrito em uma esfera pra conseguir alguma relação entre o raio e a altura do cone.
Vem com a gente que vai dar bom 😊
Passo 2
Então galera, pra começar vamos extrair uma equação relacionada à geometria do cone inscrito em uma circunferência.
A nossa secção transversal dessa situação nos dá a seguinte configuração:
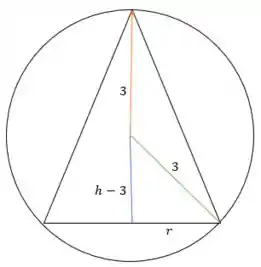
onde é o raio da esfera, a altura do cone e o raio da base do cone.
Daí, pelo teorema de Pitágoras no triângulo retângulo que apareceu lá embaixo, temos:
Logo:
Essa é a relação que precisávamos. Agora já sabemos uma relação entre e , então podemos substituir na nossa equação do volume do cone:
Substituindo...
Muito bem, agora podemos trabalhar a ideia da otimização.
Passo 3
Queremos calcular e que fazem ser o maior possível, sabendo que:
Então, podemos derivar com relação a para encontrar os pontos de máximos e mínimos da função.
Temos:
Daí, vem:
Daí, temos duas soluções:
claramente vai nos dar um ponto de mínimo, pois irá zerar o valor do volume. Sendo assim, o valor que estamos procurando para maximizar o volume é:
Pra determinar o raio da base do cone, podemos substituir na expressão que encontramos anteriormente:
Perfeito galerinha! Com isso matamos a questão 😊
Até a próxima!!