Q1. Considere todos os retângulos que possuem base contida no segmento que une os pontos e e os vértices opostos pertencentes à parábola
a) Dentre todos esses retângulos, determine o comprimento da base que possui maior área.
b) Mostre que, dentre todos esses retângulos, existem um, e apenas um, que possui diagonal medindo . Justifiqur cuidadosamente sua resposta.
Passo 1
a) Olá, pessoal! Tudo bom? Aqui nós temos um problema de otimização, onde temos que encontrar o retângulo com maior área na condição que seus vértices opostos pertençam a curva
Então antes de começar a calcular, precisamos entender de qual figura geométrica estamos falando,
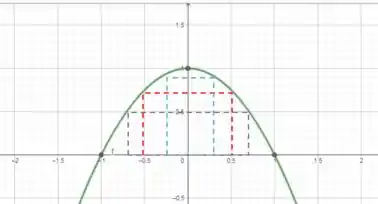
Alguns exemplos dos possíveis trigângulos estão representados em pontilhado na figura acima.
Agora temos que entender qual equação queremos otimizar!
Bora lá!
Passo 2
A área do retângulo é dada por
Como a figura é simétrica, podemos trabalhar apenas com o lado positivo. De modo queo comprimento da base será a distância da origem até a um e a altura .
Ou seja,
Para otimizar, vamos derivar essa função,
Teremos uma área máxima em um ponto crítico.
Passo 3
Igualando a zero para encontrar os pontos críticos, ficamos com
Resolvendo a equação, temos que
Logo, o comprimento da base vai de até
Prontinho! Vamos para a letra B!
Passo 4
b) Agora queremos saber qual retângulo tem a diagonal
Podemos encontrar a diagonal do retângulo pelo Teorema de Pitagoras, de modo que
Como o comprimento da base é , podemos escrever a equação assim
Essa diagonal tem que ser . Igualando,
Ajeitando a equação,
Resolvendo a equação, ficamos com duas soluções possíveis,
Ou
Entre os dois resultados apenas está dentro do segmento que une os pontos e , ou seja, é a única base possivel para obtermos essa diagonal.
Resposta
a)
b)