UTFPR - Sem Campus - Cálculo Diferencial e Integral 1 - Provas - Teste 9 - AV2 - 2022.1 - Questão 4 - Alternativa a)
Uma escada de está encostada em uma parede. Se a extremidade inferior da escada for afastada do pé da parede a uma velocidade constante de , com que velocidade a extremidade superior estará descendo no instante em que a inferior estiver a da parede?
Passo 1
Oiie, tudo certinho com você?
Temos aqui um problema de otimização, ou modelagem, ou de taxas relacionadas, pode escolher o nome que preferir. O enunciado nos dá uma escada com de comprimento encostada na parede, cuja extremidade inferior se afasta da parede com velocidade constante , como o seguinte esquema
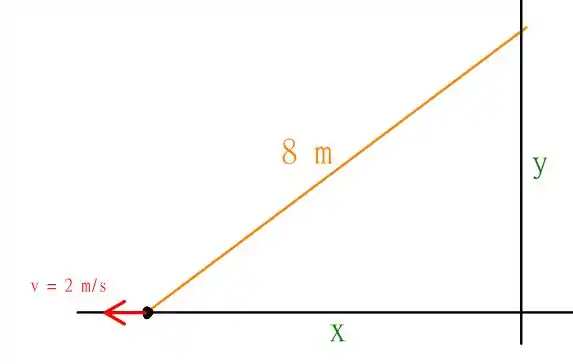
Agora, o enunciado nos pede para obter como a altura , ou seja, a velocidade com que a extremidade superior desce pela parede quando . Meio obscura a forma de resolver esse problema?
Mas tenha calma! Para isso, tudo que precisamos fazer é relacionar com de alguma forma, e calcular a derivada de em relação a . A dica que dou é, temos um triângulo retângulo, e nos foi dado o valor da hipotenusa, como achar o cateto oposto em relação ao adjacente? Captou? Vem comigo!
Passo 2
Note que como temos um triângulo retângulo, podemos relacionar os catetos com a hipotenusa usando o teorema de pitágoras, da seguinte maneira
Isolando , temos que
Podemos então tirar a raiz para obter que
Escolher o sinal positivo ou negativo aqui indica escolher se neste referencial é positivo ou negativo, portanto, por simplicidade, vamos escolher o sinal positivo! Belezinha? Maravilha! Tendo esta relação em mãos! Vamos calcular essa derivada!
Passo 3
Para calcular a derivada vamos utilizar a regra da cadeia e a regra do tombo, note que temos uma função composta da forma
Então, estou definindo que e . Pela regra da cadeia temos que
Agora, a regra do tombo é tal qual
Ou seja, com , temos a seguinte derivada
e, também temos para a outra derivada
Agora, como derivadas de constantes é sempre , e usando a regra do tombo com , temos que
Usando agora que , em que , temos que
Ou simplificando, temos que
Maravilha! Note que temos uma relação entre a derivada de e a derivada de , ou em palavras um pouco mais físicas, uma relação entre a velocidade que a extremidade superior desce pela parede e a velocidade que a extremidade inferior se afasta da parede! Utilizando os dados no enunciado agora podemos calcular o resultado desejado! Bora lá!
Passo 4
O enunciado disse que a velocidade com que a extremidade inferior se afasta é , portanto, em nossa escolha, temos que
E, é pedido para encontrar quem é quando, temos que , ou seja, utilizando a derivada que calculamos, temos
Fazendo as continhas necessárias, na calculadora, na mão, ou onde quiser, temos que
A questão foi isso! Te vejo na próxima! Tchau Tchau!