Seja T um triângulo de base B e altura H cujas ângulos internos em relação à base são agudos. Mostre que dentre todos os retângulos que podem ser inscritos nesse triângulo, o de maior volume tem base b = B/2 e altura h = H/2.
Passo 1
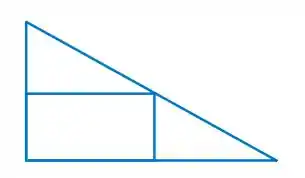 Dado o triangulo com um retângulo genérico inscrito dentro:
Dado o triangulo com um retângulo genérico inscrito dentro:
![]()
h
b
B
H
Onde a área máxima do retângulo inscrito é A = bh (1).
Passo 2
Por semelhança de triângulos, note que:
Simplificando, temos:
(2)
Substituímos em (1) e obtemos a função que descreve
ou
O ponto de máximo ou mínimo dessa função é o ponto no qual o vetor gradiente é nulo, ou seja, .
Desse modo:
-
Passo 3
Com o valor de h que maximiza a função, podemos substituir em (2) e encontrar o valor correspondente para b:
Resposta
Desse modo, o retângulo de maior volume inscrito dentro de um triangulo de base B e altura H tem base B/2 e altura H/2.