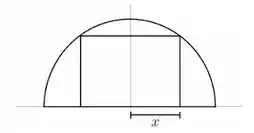
- Determine o domínio e a expressão da função que fornece a área do retângulo em termos da variável .
- Determine a área do retângulo de maior área possível que pode ser escrito em uma semicircunferência de raio e cento na origem.
Passo 1
a) Temos que determinar a expressão que representa a área do retângulo da figura em função de . Sabemos que a área de um retângulo é
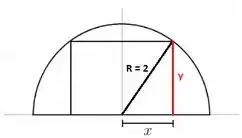
Conseguiu descobrir? Isso mesmo, vamos fazer Pitágoras e achar !
Passo 2
Agora é só unir o tudo naquela fórmula da área do retângulo. Vai ficar:
Passo 3
Falta achar o domínio dessa função que achamos pra área do retângulo. A única restrição que tem que ser feita é:
Portanto:
Mas como estamos tratando de medidas, os valores negativos e o zero não podem ser considerados, certo? Então, o domínio passa ser:
Ou
Passo 4
b) Peraí, vamos entender isso direito. O enunciado pediu pra calcular a área do retângulo de maior área possível dentro de uma semicircunferência de raio . Então ele pediu o valor MAXIMO da função área? Sim! É isso mesmo, vamos achar o valor de máximo dessa função. Pra começar temos que derivar:
Passo 5
Agora igualamos isso a zero pra encontrar os pontos críticos:
Repare que a única maneira da igualdade acima ser verdadeira é o numerador ser zero. Então podemos fazer apenas:
Passo 6
Tendo os pontos críticos, podemos fazer o teste da primeira derivada para descobrir se são máximos ou mínimos. Observe que na expressão
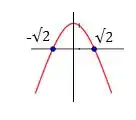
- O sinal é negativo antes de e depois fica positivo, portanto esse ponto é um mínimo local
- O sinal é positivo antes de e depois fica negativo, portanto esse ponto é um máximo local
Passo 7
Agora que descobrimos o ponto de máximo podemos substitui-lo na função da área, assim, encontrar a maior área possível.
Resposta
a) e
b) u.a