Num motor a combustão, uma biela de tem uma de suas extremidades acoplada a uma manivela cujo raio é de . Na outra extremidade da biela está um pistão que se move quando a manivela gira (vide Figura abaixo). Sabendo que a manivela gira no sentido anti-horário a uma taxa constante de rotações por minuto, calcule a velocidade do pistão quando o ângulo de rotação do disco é (medido a partir da posição em que o pistão está mais afastado do disco).
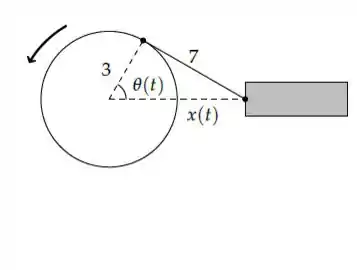
Passo 1

Mas espera aí! Sabemos a lei dos cossenos! Aplicando no nosso esquema temos
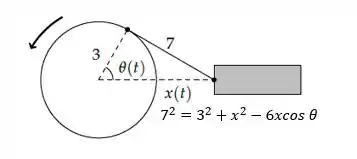
Então vamos derivar dos dois lados em relação ao tempo e substituir nos dados!
Tranquilo? Relaxa, vou fazer passo a passo contigo!

Bora lá!
Passo 2
Derivando a lei dos cossenos
Agora vamos os dados:
Quando temos que é
Aplicando a formula de bascara, temos duas raízes: uma positiva e outra negativa. Vamos pegar apenas a positiva
E multiplicando a frequência por temos :
Beleza?

Agora é só substituir na derivada
Assim, isolando temos
 E é isso! Até a próxima!
E é isso! Até a próxima!