- Uma peça mecânica é construída a partir de uma esfera de raio R na qual faz-se um pequeno furo cilíndrico cujo eixo de simetria passa exatamente pelo centro da esfera. Determine o raio do furo para o qual a área total seja máxima.
Passo 1
Olá, galerinhaa!!! Vamos lá? Aqui nesta questão, vamos tratar de um problema de otimização.
Mas o que é otimizar?
Bom, otimizar significa chegar ao ótimo, à melhor situação possível. Em Cálculo 1 isso implica dizer que vamos ter uma situação que pode ser descrita por uma função , e vamos procurar um , de tal forma que
Esse ponto representa o cenário ideal que buscamos alcançar.
Ah, e mais uma coisa antes de passarmos pra questão em si, otimizar pode tanto significar obter o máximo quanto o mínimo de uma situação. Agora vamos pra nossa questão.
Passo 2
Vamos agora observar a seguinte imagem, que representa uma visão superior a peça
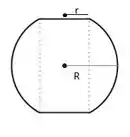
Se usarmos um pouco da nossa imaginação conseguiremos ver que a área da peça é a área da superfície esférica, mais a área do cilindro formado no interior da esfera menos a área das “tampas” do cilindro. Ou seja,
Passo 3
Vamos agora derivar a nossa função. Assim,
Agora, igualamos a derivada a 0, e
Logo, o raio ideal é se
Por hoje é isso pessoal, terminamos 😅😅. Até a próximaa!!
Resposta