Um galpão deve ser construído com uma área retangular de . E necessário que haja um recuo de 25 m na frente, 15 m na parte traseira e 5 m em cada lado. Encontre as dimensões do lote de área mínima na qual tal galpão pode ser construído. Faça um esboço da situação.
Passo 1
Oieee,
Vamos resolver o problema por definição, considerando as restrições dadas. Primeiro, vamos criar um esboço da situação para visualizar melhor o problema:
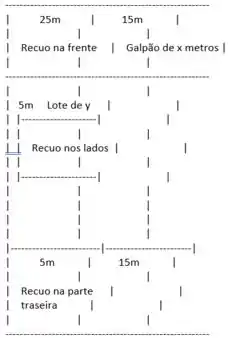
A área total do lote é de 8100 m², e as dimensões do galpão são x metros de largura e y metros de comprimento. Portanto, a área do lote é dada por:
Agora, você deseja encontrar as dimensões do lote (x e y) que minimizam essa área. No entanto, existem duas restrições importantes:
1. Recuo na frente: 25 metros
2. Recuo na parte traseira: 15 metros
3. Recuo nos lados: 5 metros de cada lado
Passo 2
Essas restrições implicam que a largura efetiva do lote é metros, e o comprimento efetivo do lote é metros.
Portanto, você tem as seguintes restrições:
1. (largura efetiva não pode ser negativa)
2. (comprimento efetivo não pode ser negativo)
A área do lote efetiva, sujeita a essas restrições, é:
Agora, você deseja minimizar a área efetiva do lote sujeita às restrições. Vamos abordar isso usando um método gráfico. Primeiro, vamos traçar as restrições no plano cartesiano:
1. (lado esquerdo do lote)
2. (parte traseira do lote)
3.
Passo 3
Agora, vamos resolver o sistema de inequações e encontrar o ponto onde a área é minimizada:
Primeiro, a restrição implica que
Segundo a restrição implica que
Agora, podemos encontrar o ponto onde a área é minimizada:
Agora, resolvendo essa equação:
Expandindo:
Reorganizando:
Passo 4
Agora, vamos traçar essa equação juntamente com as restrições no plano cartesiano:
- A linha azul representa a restrição (lado esquerdo do lote).
- A linha vermelha representa a restrição (parte traseira do lote).
- A curva verde representa a equação
Vamos encontrar o ponto de interseção entre as três curvas, que representará as dimensões do lote que minimizam a área:
Aqui está o esboço da situação:
```
^
y |-----------------------
| \ /
| \ /
| \ /
| \ /
|-------\/-----------
|
|-----------------------
|
+------------------------>
x
Resposta
Vide a explicação.