Questão 2:
Considere um triângulo com um vértice no ponto e outros dois vértice, e , pertencentes à curva de equação . As seguintes condições devem ser satisfeitas:
- O lado é paralelo ao eixo .
- A abscissa (coordenada ) do vértice é maior que as abscissas dos vértices e .
- A ordenada (coordenada ) do vértice é maior que a ordenada do vértice .
Seja a abscissa do vértice .
- Determine o domínio e a expressão da função que fornece a área do triângulo em termos de .
- Determine a área do triângulo que tem área máxima.
Obs.: Respostas sem justificativas não serão aceitas.
Passo 1
Vamos começar aqui desenhando esse tal triângulo de acordo com as condições do enunciado. Pois bem, sabemos que ele tem dois vértices, e sob a parábola ... O outro ponto é o .
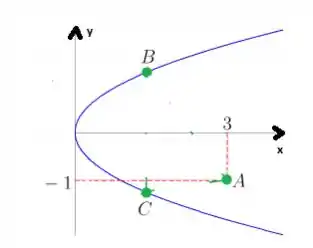
O problema nos disse que o lado é paralelo ao eixo ...
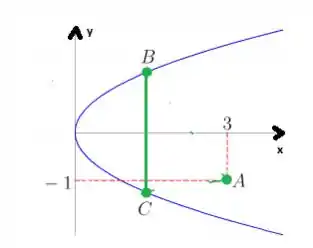
E que a coordenada de é sempre maior que as coordenadas dos outros vértices, ou seja, o triângulo sempre está do lado esquerdo de .
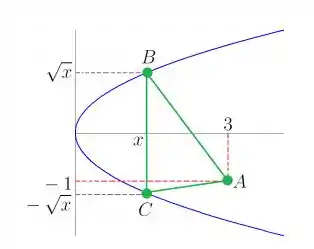
A outra informação, de que a ordenada de é maior do que a de , é só para indicar que o está lá em cima, como no desenho.
Passo 2
Bem, se você falar que o lado passa por , a ordenada do será...
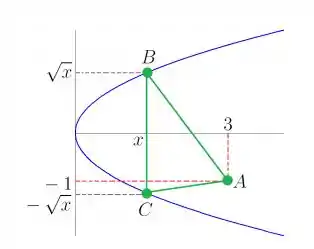
O Domínio da função área será sempre até a coordenada pode ir, ou seja... De até ...
Passo 3
Para determinar a função área, bem... É só calcularmos a área desse triângulo aqui:
Se considerarmos a base essa retinha paralelo ao , o seu tamanho é...
Enquanto que á altura será...
Passo 4
O que precisamos fazer aqui é otimizar a função área. Para fazer isso, vamos buscar pelos pontos críticos, ou seja, pontos que satisfaçam...
Derivando a função área aplicando a regra do produto...
Passo 5
O único que zera essa derivada é...
Esse é único ponto crítico e, portanto, o único candidato a ponto de máximo. Apenas temos que verificar se isso é verdade, analisando o sinal da primeira derivada...
A função é sempre positiva, logo o único sinal que manda em tudo é o sinal de
E isso implica em
Quando
Como sabemos que
Então de fato se antes de , temos a função crescendo e depois de a função decrescendo, o , é justamente o ponto de maior valor, saca?
Então essa é a maior área possível !