USP– Cálculo 1 – Lista 1 – Questão 5.9b
Uma escada de bombeiro com está encostada na parede de um prédio e sua base se afasta da parede. Num certo instante, a base da escada se encontra a da parede e sua velocidade é de .
b) Considere o triângulo formado pela parede da casa, a escada e o chão. Calcule a taxa de variação da área deste triangulo no instante em que a base da escada se encontra a da parede.
Passo 1
Mas espera aí! Quando a escada esta encostada no prédio ela vira forma um triângulo retângulo, saca só
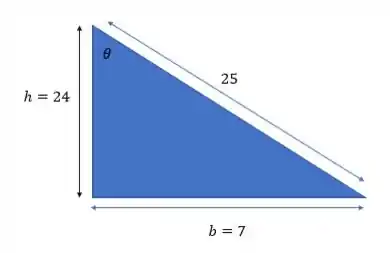
E pelo teorema de Pitágoras
Certo? E mais do que isso, sabemos também a área
Então vamos derivar a área dos dois lados em relação ao tempo e substituir nos dados!
Tranquilo? Relaxa, vou fazer passo a passo contigo!
Bora lá!
Passo 2
Derivando a fórmula que relaciona a área, base e altura
Agora vamos os dados:
Pelo desenho, quando a hipotenusa é e a base é , como no nosso caso, o outro cateto (altura) é
agora as taxas:
Passo 3
Agora é só substituir!
E é isso! Até a próxima!