UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Derivadas, Questão 8.10
Uma lata cilíndrica sem topo é feita para receber de líquido. Encontre as dimensões que minimizarão o custo do metal usado para fazer a lata.
Passo 1
Eaee!!! Belezinha? Bom... Para encontrar as dimensões que minimizarão o custo do metal usado para fazer a lata cilíndrica, precisamos otimizar a área de superfície da lata.
Vamos supor que o raio da base do cilindro seja e a altura seja :
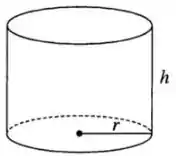
A área de superfície da lata cilíndrica é composta por duas partes: a área da base circular e a área lateral :
Assim a área total da lata é dada por:
Para minimizarmos o custo do metal que será utilizado, temos que derivar a área total em função do raio e igualar a zero.
Mas antes, precisamos encontrar essa expressão!
E aí? Bora lá??
😉
Passo 2
Bom... sabemos que o volume da lata é dado por:
Isolando uma das variáveis, temos:
Substituindo na fórmula da área total, temos:
Passo 3
Agora, para minimizar , devemos derivar a expressão e igualar a zero:
Substituindo em :
Entendeu direitinho? Responde aee ;)
