Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Otimização

Ver Teoria
Exercício 621234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606163646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFRJ – Cálculo 1 – Lista 13 – Questão 4

Uma janela normanda tem a forma de um retângulo tendo em cima um semicírculo. (O diâmetro do semicírculo é igual à largura do retângulo). Se o perímetro da janela for 10   m , encontre as dimensões da janela que deixam passar a maior quantidade possível de luz.

Passo 1

Com as informações do enunciado a gente faz a seguinte figura:

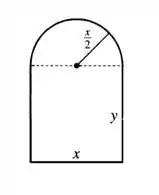
Passo 2

O exercício pede as dimensões da janela que permitem a maior ÁREA de luz possível, então é essa fórmula que a gente vai maximizar:

A = x y + 1 2 π x 2 2 = x y + x 2 π 8

A outra informação que a gente tem é o perímetro de 10   m , aí dá pra anotar mais uma fórmula:

P = x + 2 y + 2 π x 2 2 = x + 2 y + π x 2 = 10

Com essa fórmula do perímetro a gente consegue isolar uma das variáveis, pra depois maximizar a área e finalmente encontrar as dimensões!!

x + 2 y + π x 2 = 10

2 y = 10 - x - π x 2

y = 5 - x 2 - π x 4

Substituindo y   em A :

A = x y + x 2 π 8

A = 5 x - x 2 2 - x 2 π 8

Passo 3

Maximizando A :

A ' x = 0 = 5 - x - 1 4 π x

A ' x = 0 = 5 - x ( 1 + 1 4 π )

x = 5 1 + 1 4 π

x = 20 4 + π

Substituindo em y :

y = 5 - x 2 - π x 4

y = 5 - 20 2 4 + π - π   ( 20 4 4 + π )

y = 5 - 10 4 + π - 5 π 4 + π

y = 10 4 + π

Como podemos constatar, a altura do retângulo é metade de sua largura.

Resposta

Dimensões máximas: x = 20 4 + π e y = 10 4 + π

Exercícios de Livros Relacionados

Encontre a área do maior retângulo que pode ser inscrito na elipse x 2 a 2 + y 2 b 2 = 1
Um modelo usado para a produção Y de uma colheita agrícola como função do nível de nitrogênio N no solo (medido em unidades apropriadas) é Y = k N 1 + N 2 Em que k é um constante positiva. Que nível d
Gerentes de lojas querem uma política de estoque ótima. Excesso de estoque resulta em armazenagem excessiva e custos de estoque, enquanto que um estoque pequeno significa adicionar custo à reorganizaç
Um cilindro circular reto é inscrito em uma esfera de raio r . Encontre o maior volume possível para este cilindro.
Um cilindro circular reto é inscrito em um cone com altura h e raio da base r . Encontre o maior volume possível para este cilindro.