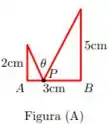
Como deve ser escolhido o ponto P na figura (A) abaixo de modo que o ângulo seja máximo?
Passo 1
Iai galerinha, suave? Para respondermos essa questãozinha, vamos começar analisando a figura e fazendo um estudo de seus ângulos e do lado AB, da seguinte maneira:
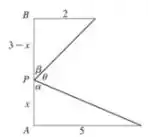
Passo 2
Belezinha, agora, vamos continuar. Como o que queremos é encontrar o valor máximo para , então, vamos buscar uma fórmula para , para depois, utilizando os conhecimentos de derivada e de suas aplicações, acharmos esse valor máximo.
- Sabemos que: ou
- Pela análise da figura, também conseguimos os valores de e , que serão:
- Logo:
e
e
Passo 3
Para calcular seu valor máximo, vamos precisar achar a derivada de , e depois igualarmos a 0. Então vamos colocar a mão na massa:
Como x só vai variar entre 0 e 3, que é exatamente o tamanho do lado AB, só vamos ter uma única raiz possível, sendo ela: .
Agora, por fim, só jogarmos substituirmos pelo valor que interpretamos na figura, para acharmos a que distância o ponto P deve estra colocado do ponto A:
Resposta
P deve estar colocado a cm do ponto A.