UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Derivadas, Questão 8.2
Determine o retângulo de maior área e lado paralelos aos eixos coordenados que está inscrito na elipse .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos diz para determinar a maior área de lados paralelos de um retângulo inscrito na elipse dada por:
Graficamente, temos:
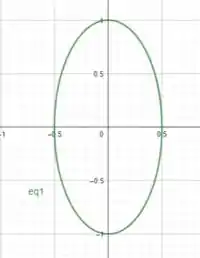
Para descobrirmos esse retângulo, primeiramente precisamos aplicar a equação da elipse na equação da área do retângulo.
Para isso, como queremos encontrar a área máxima, iremos derivar e igualar a equação resultante a zero para descobrirmos os pontos.
Eita... muita informação, né?
Então vamos devagarinho aqui que vai dar certo!!
😉
Passo 2
Bom...sabemos que a área de um retângulo é dada pelo produto da sua base por sua altura :
Passando para os valores das coordenadas, podemos interpretar a área da seguinte forma:
Por outro lado, podemos isolar o na equação da elipse:
Substituindo na equação da área do retângulo, temos:
Reorganizando, temos:
Passo 3
Derivando a equação, temos:
Aplicando a Regra da Cadeia, temos:
Igualando a zero, temos:
Passo 4
Agora, substituindo os valores de na equação da elipse, podemos encontrar os valores de :
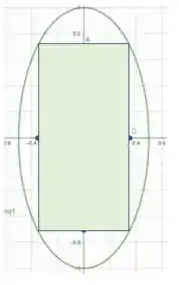
Assim, plotando no gráfico, vamos ter o seguinte retângulo inscrito:
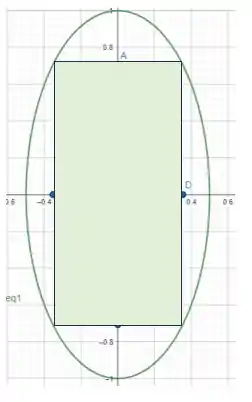
Entendeu direitinho? Responde aee ;)
Resposta
