UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Derivadas, Questão 8.4
Um fazendeiro tem de cerca para construir três galpões retangulares adjacentes e com lados medindo e . Quais devem ser as dimensões dos galpões de modo a maximizar a área total cercada?
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para determinar as dimensões de três galpões adjacentes de forma que o seu perímetro máximo seja de .
Primeiramente, vamos desenhar os galpões:
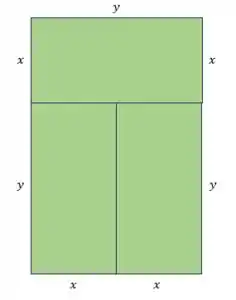
Através da figura, percebemos que seu perímetro é dado por:
Ou seja, como seu perímetro máximo deve ser de , então:
Agora, temos que relacionar esse perímetro com a área do retângulo e derivarmos em seguida igualando a zero para encontrarmos o ponto máximo!
Então vamos devagarinho aqui que vai dar certo!!
😉
Passo 2
Bom...pela figura, vemos que a área é dada por:
Isolando na equação do perímetro, temos:
Substituindo na equação da área:
Derivando a equação, temos:
Agora vamos derivar e igualar a zero!!
Passo 3
Igualando a equação da área a zero a fim de encontrarmos o ponto máximo, temos:
Substituindo na equação do perímetro, temos:
Dessa forma, temos as dimensões de cada galpão e .
Entendeu direitinho? Responde aee ;)
