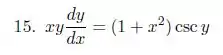
Passo 1
A primeira coisa que ele mandou fazer no problema é verificar se a equação é separável e para isso precisamos colocar a equação naquele formato característico.
Vamos manipular a equação e ver se é possível fazer isso.
Agora é só resolver.
Passo 2
Integrando a parte esquerda da equação.
Tomando e podemos resolver essa integral utilizando integração por partes. Lembrando a fórmula.
Lembrando que nós deixamos para adicionar a constante de integração depois que igualarmos as equações.
Passo 3
Integrando a parte direita da equação.
Passo 4
Igualando as integrais e somando uma constante
Temos, então, a solução implícita do problema.
Resposta
Exercícios de Livros Relacionados
De acordo com a Lei da Gravitação Universal de Newton, a força gravitacional em um objeto de massa m que tenha sido lançado verticalmente para cima da superfície da Terra é F = m g R 2 x + R 2 onde x
y ' = x 2 y (a) Use um sistema de computação algébrica para desenhar um campo de direções para a equação diferencial. Imprima-o e esboce algumas curvas solução sem resolver a equação diferencial.(b) R
Resolva a equação diferencial x y ' = y + x e y x usando a mudança de variáveis v = y x .
Resolva o problema de valor inicial y ' = s e n x s e n y, y 0 = π 2, e trace a solução (se seu SCA fizer gráficos implícitos).
Uma esfera com raio de 1m está a uma temperatura de 15° C . Ela está dentro de uma esfera concêntrica com raio de 2m e temperatura de 25° C . A temperatura T r a uma distância r do centro comum das du