UTFPR, Sem Campus, Cálculo Diferencial e Integral 2, Listas de Cálculo 2 - Profº Félix Gómez - Primeira Lista, Questão 2.2e
Encontre o domínio e a imagem da função e trace um esboço mostrando uma região sombreada em , como um conjunto de pontos no domínio de .
Passo 1
Fala aí pessoal, tudo beleza?
Nessa questão estamos trabalhando com as queridíssimas funções de duas variáveis.
Recebemos a função:
E, precisamos calcular o seu domínio e a sua imagem.
Vocês lembram o que é o domínio e o que é a imagem?
É legal pensar numa analogia da função como sendo uma liquidificador. O domínio é o conjunto de todos os ingredientes que você pode colocar dentro do liquidificador (não dá pra colocar tudo, algumas coisas quebraria o aparelho, certo?).
Já a imagem é o que o liquidificador produz após bater todos aqueles ingredientes, sacaram?
Então, nossa ideia é primeiro verificar as possíveis restrições na nossa lei de função para encontrar o domínio de .
Em seguida, vemos os possíveis valores que esse domínio pode nos dar em .
Vem com a gente que vai ficar bem claro 😊
Passo 2
Bom, vamos analisar a nossa função:
Como trata-se de uma fração, a possível restrição seria o denominador ser diferente de zero.
Assim:
Daí, podemos escrever o domínio como sendo:
Ou seja, o nosso domínio é todo o plano dos reais, exceto pelos eixos e .
Podemos representar essa região como:
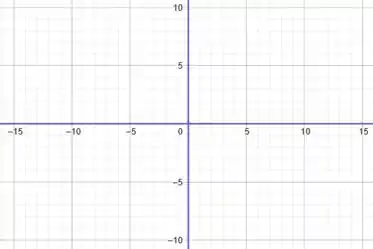
Excelente!
Passo 3
Pensando agora na imagem da função , vamos pensar um pouco no que temos:
Como temos uma fração, pensar no menor valor possível para o denominador.
Se tivermos:
E:
O nosso numerador é diferente de zero, mas o denominador está muito próximo de zero. Assim, a nossa função vai tender pro infinito.
Assim, escolhendo bem o valor de , temos:
- Valor máximo:
- Valor mínimo:
Assim, temos a imagem:
Valeeeu pessoal, até a próxima 😊