UTFPR, Sem Campus, Cálculo Diferencial e Integral 2, Listas de Cálculo 2 - Profº Félix Gómez - Primeira Lista, Questão 2.1d
Seja a função, e o conjunto
Resolva as questões,
a seguir trace um esboço mostrando como um sólido sombreado em , o conjunto de pontos do domínio de .
Passo 1
Fala aí pessoal, tudo bom com vocês?
Nessa questão temos uma função , que foi dada de uma forma meio diferente no enunciado. Então, vamos começar tentando entender melhor quem é essa função.
Foi dito que:
Isso significa que o domínio de é um ponto do , por exemplo e que o contradomínio de está nos reais. Ou seja, recebe um ponto do e devolve um número real.
Também foi falado que:
Basicamente, o ponto é um ponto do . Se aplicarmos esse ponto em , vamos ter:
O resultado é um número real, que é justamente a imagem da nossa função .
Conseguiram entender?
Nesse contexto precisamos calcular o domínio da função . Ou seja, encontrar o conjunto de pontos que representa o domínio de .
Depois disso, iremos traçar um esboço do sólido que representa o domínio de .
Vem com a gente 😊
Passo 2
Vimos que o domínio de é dado por um ponto no tal que:
Beleza?! Mas, o valor que irá retornar é dado pela expressão:
Precisamos investigar as restrições que podem ocorrer nessa expressão em função dos valores de e .
Como trata-se de uma raiz quadrada, sabemos que o termo no seu interior não pode ser negativo. Ou seja:
Daí:
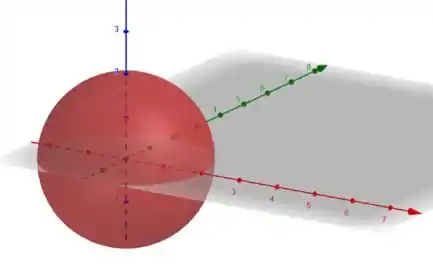
Essa é justamente a equação de uma esfera no , centrada em e cujo raio vale .
Isso significa que os pontos que pertencem ao domínio de estão na superfície ou no interior dessa esfera.
Logo, o domínio de pode ser escrito como:
Além disso, esboçando essa esfera no , temos a seguinte figura:
Prontinho! Com isso finalizamos a questão!
Valeeu pessoal 😊