UTFPR, Sem Campus, Cálculo Diferencial e Integral 2, Listas de Cálculo 2 - Profº Félix Gómez - Primeira Lista, Questão 2.2a
Encontre o domínio e a imagem da função e trace um esboço mostrando uma região sombreada em , como um conjunto de pontos no domínio de .
Passo 1
Fala aí gente, tudo na paz?
Nessa questão estamos trabalhando com as queridíssimas funções de duas variáveis.
Recebemos a função:
E, precisamos calcular o seu domínio e a sua imagem.
Vocês lembram o que é o domínio e o que é a imagem?
É legal pensar numa analogia da função como sendo uma liquidificador. O domínio é o conjunto de todos os ingredientes que você pode colocar dentro do liquidificador (não dá pra colocar tudo, algumas coisas quebraria o aparelho, certo?).
Já a imagem é o que o liquidificador produz após bater todos aqueles ingredientes, sacaram?
Então, nossa ideia é primeiro verificar as possíveis restrições na nossa lei de função para encontrar o domínio de .
Em seguida, vemos os possíveis valores que esse domínio pode nos dar em .
Vem com a gente que vai ficar bem claro 😊
Passo 2
Bom, vamos analisar um pouco a nossa função :
Temos duas partes nela que são candidatas a problema. A primeira é a raiz quadrada, pois o termo dentro da raiz não pode ser negativo. Assim:
Isso é a equação de uma circunferência, que está centrada em e que possui raio igual a:
Massa! Então, o conjunto de pontos que satisfazem a nossa raiz estão dentro ou na borda da circunferência citada.
Além disso, a segunda parte que é candidata a problema é que temos um denominador. E, como sabemos, não podemos nunca dividir por zero. Ou seja, o denominador precisa ser não nulo:
Daí, o nosso domínio pode ser representado da seguinte forma:
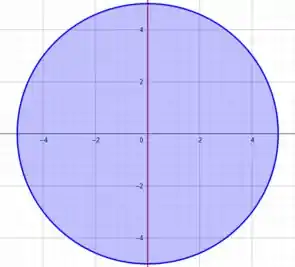
onde toda a região interna pertence ao domínio, exceto pela reta vermelha em .
Podemos também escrever formalmente esse domínio como sendo:
Excelente!
Passo 3
Agora vamos verificar a imagem da nossa função. Temos:
Vamos começar pensando nos valores máximos, em módulo, que a função pode atingir.
Como o denominador pode-se aproximar de o tanto quanto possível, a função deve ter para o infinito.
Vamos pensar agora nos valores mínimos.
Se o numerador zerar, a nossa função assumirá o menor valor possível.
Se tivermos , ficamos com:
Logo, o menor valor que a função pode assumir é:
Portanto, a imagem da nossa função é:
É isso galera!
Espero que vocês tenham curtido, até a próxima 😊